73 min read

11 Oct

11Oct

Inorganic Chemistry

Course Description:

This course provides a comprehensive introduction to the principles and applications of inorganic chemistry. It covers fundamental concepts such as atomic structure, chemical bonding, and molecular symmetry, and explores the chemistry of main group and transition metal elements. Topics include acid-base chemistry, coordination chemistry, organometallic chemistry, and solid-state inorganic chemistry. The course emphasizes understanding the periodic trends in chemical properties and the reactivity of inorganic compounds, with a focus on their applications in various fields such as catalysis, materials science, and biochemistry.

Course Objectives:

Upon successful completion of this course, students will be able to:

Describe the fundamental principles of atomic structure and chemical bonding.
Apply concepts of molecular symmetry and group theory to understand molecular properties.
Explain periodic trends in the physical and chemical properties of elements.
Discuss the chemistry of main group elements, including their synthesis, reactivity, and applications.
Analyze the structure, bonding, and reactions of coordination compounds.
Understand the basic principles of organometallic chemistry and its industrial applications.
Elucidate the principles of acid-base chemistry in inorganic systems.
Describe the structures and properties of solid-state inorganic materials.
Relate inorganic chemistry concepts to real-world applications in various scientific and technological fields.
Solve problems involving inorganic reactions, structures, and properties.

TABLE OF CONTENT:

Chapter 1: Introduction to Inorganic Chemistry and Atomic Structure

This chapter will introduce the scope and importance of inorganic chemistry. We will delve into the fundamental concepts of atomic structure, reviewing quantum mechanics and atomic orbitals. Key topics include quantum numbers, electron configurations, and the Aufbau principle. The chapter will also cover the historical development of atomic theory and the experimental evidence that led to our current understanding of the atom. We will explore how atomic structure dictates the chemical properties of elements.

Chapter 2: Periodic Trends and Chemical Bonding

Building on atomic structure, this chapter will explore periodic trends in atomic and ionic radii, ionization energy, electron affinity, and electronegativity. We will then transition into the various types of chemical bonding: ionic, covalent, and metallic. Valence Bond Theory (VBT) and Molecular Orbital Theory (MOT) will be introduced as frameworks for understanding covalent bonding, including concepts like hybridization and resonance. The role of intermolecular forces in determining bulk properties will also be discussed.

Chapter 3: Molecular Symmetry and Group Theory

This chapter introduces the concept of molecular symmetry, a powerful tool for understanding and predicting molecular properties. We will learn about symmetry elements (identity, rotation axes, mirror planes, inversion center) and symmetry operations. Point groups will be assigned to various molecules, and we will explore the basics of group theory, including character tables and irreducible representations. Applications of symmetry in spectroscopy and bonding will be briefly touched upon.

Chapter 4: Acid-Base Chemistry in Inorganic Systems

This chapter will broaden the traditional understanding of acid-base chemistry to encompass inorganic systems. We will review Brønsted-Lowry and Lewis acid-base theories and then explore Lux-Flood, Usanovich, and solvent system concepts. The concept of hard and soft acids and bases (HSAB theory) will be introduced, providing a framework for predicting the stability of complexes and the outcomes of reactions. Practical applications in inorganic synthesis will be highlighted.

Chapter 5: Chemistry of Main Group Elements I (Groups 1, 2, 13, 14)

This chapter begins our detailed exploration of the chemistry of main group elements. We will cover the trends in properties, reactivity, and common compounds of Group 1 (alkali metals) and Group 2 (alkaline earth metals). Their characteristic reactions, especially with water and halogens, will be examined. We will then move to Group 13 (boron group) and Group 14 (carbon group), focusing on the unique chemistry of boron (e.g., boranes) and the allotropes and diverse compounds of carbon and silicon.

Chapter 6: Chemistry of Main Group Elements II (Groups 15, 16, 17, 18)

Continuing with the main group, this chapter focuses on Groups 15 (nitrogen group), 16 (chalcogens), 17 (halogens), and 18 (noble gases). For Group 15, we will discuss the diverse oxidation states of nitrogen and phosphorus and the chemistry of their hydrides, oxides, and halides. For Group 16, we will explore oxygen and sulfur chemistry, including their allotropes and important compounds. The halogens will be covered in terms of their reactivity and the properties of interhalogen compounds. Finally, the increasingly rich chemistry of noble gas compounds will be discussed.

Chapter 7: Introduction to Transition Metal Chemistry and Ligand Field Theory

This chapter introduces the transition metals, emphasizing their unique properties such as variable oxidation states, colorful compounds, and catalytic activity. We will discuss their electron configurations and common oxidation states. The core of this chapter will be Ligand Field Theory (LFT), an extension of crystal field theory, which explains the bonding, magnetic properties, and electronic spectra of transition metal complexes. Concepts like crystal field splitting, high-spin/low-spin complexes, and Jahn-Teller distortion will be covered.

Chapter 8: Coordination Chemistry: Structure, Isomerism, and Reactivity

Building on LFT, this chapter delves deeper into coordination chemistry. We will examine the various geometries of coordination complexes, including square planar, tetrahedral, and octahedral. Different types of isomerism in coordination compounds (e.g., geometric, optical, linkage, hydration, ionization) will be discussed with examples. The chapter will also cover the basic principles of ligand substitution reactions and electron transfer reactions in coordination complexes.

Chapter 9: Organometallic Chemistry: Fundamentals and Applications

This chapter introduces the fascinating field of organometallic chemistry, which bridges inorganic and organic chemistry. We will discuss the nature of the metal-carbon bond and explore common organometallic ligands (e.g., carbonyls, alkyls, alkenes, cyclopentadienyls). The 18-electron rule will be introduced as a guideline for predicting stability. Key reactions in organometallic chemistry, such as oxidative addition, reductive elimination, insertion, and β-hydride elimination, will be covered, along with important catalytic cycles like the Monsanto acetic acid process or olefin polymerization.

Chapter 10: Solid-State Inorganic Chemistry and Materials Science

The final chapter explores the structures and properties of solid-state inorganic materials. We will discuss different types of solids (ionic, covalent network, molecular, metallic) and their characteristic features. Crystal structures, including common unit cells (e.g., NaCl, CsCl, perovskite), will be examined. Concepts like defects in solids, non-stoichiometry, and band theory will be introduced to explain the electronic and optical properties of materials. The chapter will conclude with an overview of important inorganic materials, such as superconductors, semiconductors, and catalysts, and their applications.

CHAPTER 1:

Inorganic chemistry is a vast and fascinating field that explores the synthesis, reactions, structures, and properties of compounds that are not carbon-hydrogen based. While organic chemistry focuses on hydrocarbons and their derivatives, inorganic chemistry encompasses all other elements and their compounds, including metals, nonmetals, and metalloids. This diverse discipline is crucial for understanding a wide range of phenomena, from the minerals that form the Earth's crust to the catalysts used in industrial processes and the metal ions essential for biological functions.

The importance of inorganic chemistry cannot be overstated; it underpins advancements in materials science, medicine, environmental science, and energy production. For instance, the development of new battery technologies relies heavily on understanding the inorganic compounds involved in energy storage and transfer. The discovery of platinum-based anticancer drugs like cisplatin revolutionized cancer treatment, demonstrating the profound impact of inorganic compounds on human health.At the heart of understanding inorganic chemistry lies a firm grasp of atomic structure. Our current model of the atom, while incredibly sophisticated, is the culmination of centuries of scientific inquiry and experimental evidence. Early models, like Dalton's indivisible spheres, were groundbreaking but limited. J.J. Thomson's discovery of the electron led to the "plum pudding" model, where negative electrons were embedded in a positively charged sphere. This was soon superseded by Rutherford's nuclear model, which proposed a dense, positively charged nucleus surrounded by electrons orbiting in a vast empty space.

However, Rutherford's model couldn't explain why electrons didn't spiral into the nucleus or the discrete spectral lines observed when elements were excited.The breakthrough came with the advent of quantum mechanics, a revolutionary theory that describes the behavior of matter and energy at the atomic and subatomic levels. Niels Bohr applied quantum principles to the atom, proposing that electrons exist in specific, quantized energy levels or orbits. While Bohr's model successfully explained the hydrogen spectrum, it failed for more complex atoms.

The more refined and widely accepted quantum mechanical model of the atom treats electrons not as particles orbiting the nucleus in fixed paths, but as wave-like entities occupying regions of space called atomic orbitals.Atomic orbitals are mathematical functions that describe the probability of finding an electron in a particular region around the nucleus. Each orbital has a unique shape and energy, characterized by a set of quantum numbers. There are four main quantum numbers:

Principal Quantum Number (n): This number describes the electron's main energy level and its distance from the nucleus. It can take on positive integer values (1, 2, 3, ...). Higher values of n indicate higher energy levels and larger orbitals. For example, an electron with n = 1 is in the first shell, closest to the nucleus, while an electron with n = 2 is in the second shell, further out and at a higher energy.
Azimuthal or Angular Momentum Quantum Number (l): This number describes the shape of the atomic orbital and is related to the sublevel within a principal energy level. Its values range from 0 to n- 1.
- l = 0 corresponds to an s orbital, which is spherical.
- l = 1 corresponds to a p orbital, which is dumbbell-shaped.
- l = 2 corresponds to a d orbital, which has more complex shapes (often cloverleaf).
- l = 3 corresponds to an f orbital, with even more intricate shapes.
  For example, for n = 2, l can be 0 or 1, meaning the second shell contains s and p sublevels.
Magnetic Quantum Number (ml): This number describes the orientation of the orbital in space. Its values range from -l to +l, including 0.
- For l = 0 (s orbital), ml = 0, meaning there is only one s orbital per sublevel.
- For l = 1 (p orbitals), ml = -1, 0, +1, meaning there are three p orbitals (px, py, pz) oriented along different axes.
- For l = 2 (d orbitals), ml = -2, -1, 0, +1, +2, meaning there are five d orbitals.
Spin Quantum Number (ms): This number describes the intrinsic angular momentum of an electron, often visualized as its "spin." Electrons behave as if they are spinning, generating a magnetic field. There are two possible spin orientations: +1/2 (spin up) and -1/2 (spin down).

These quantum numbers provide a unique "address" for each electron in an atom. According to the Pauli Exclusion Principle, no two electrons in an atom can have the same set of four quantum numbers. This means that each atomic orbital can hold a maximum of two electrons, and those two electrons must have opposite spins.The arrangement of electrons in an atom's orbitals is known as its electron configuration. This configuration dictates the chemical behavior of an element. We determine electron configurations using the Aufbau principle, which states that electrons fill orbitals starting from the lowest energy level first. The order of filling is generally 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, and so on.Let's illustrate with practical examples:Example 1: Hydrogen (H)

Hydrogen has 1 electron.

n = 1 (first shell)
l = 0 (s orbital)
ml = 0 (one orientation)
ms = +1/2 (spin up)
Electron configuration: 1s¹
This means the single electron occupies the 1s orbital.

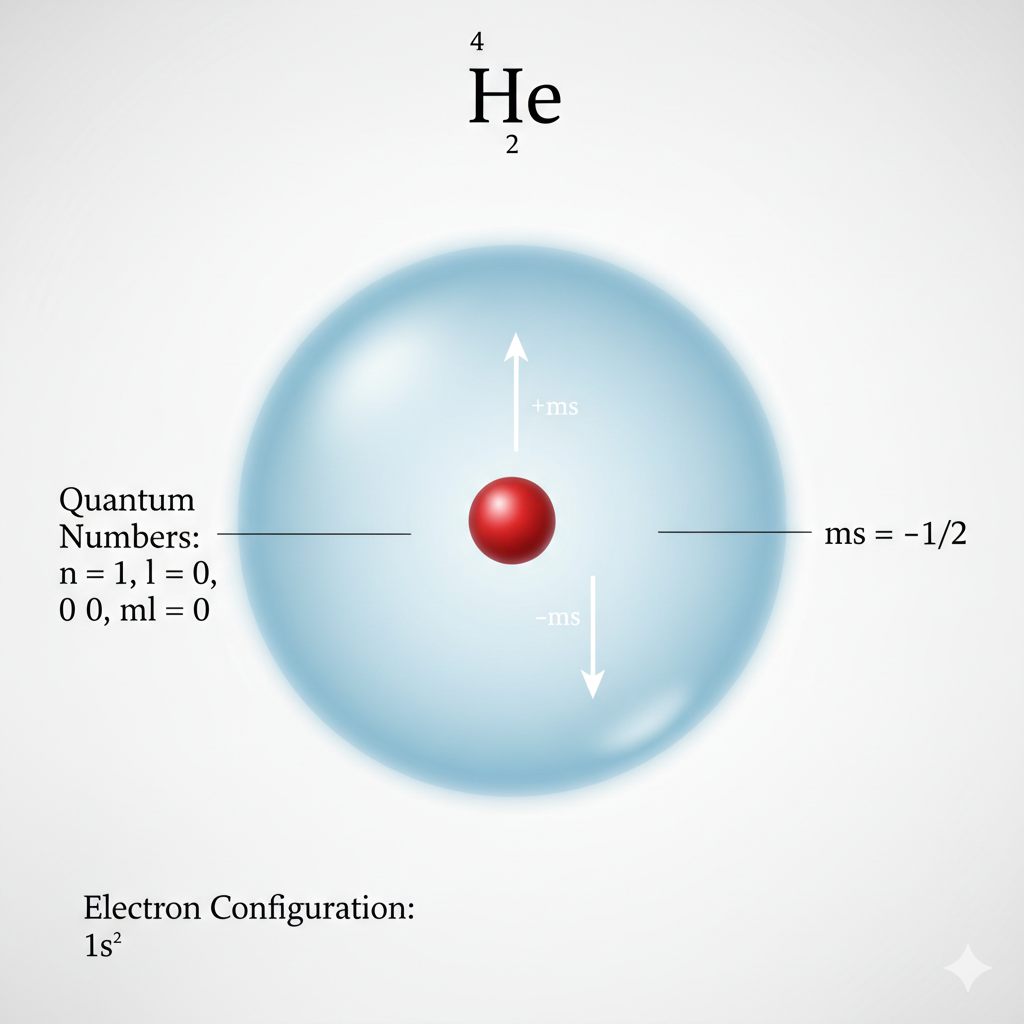
Example 2: Helium (He)
Helium has 2 electrons.
The first electron: 1s¹, with ms = +1/2.
The second electron must also go into the 1s orbital, but with opposite spin due to the Pauli Exclusion Principle.
The second electron: 1s¹, with ms = -1/2.
Electron configuration: 1s²
Helium's full 1s orbital makes it exceptionally stable and unreactive.

Example 3: Oxygen (O)

Oxygen has 8 electrons.

Following the Aufbau principle:

First two electrons fill the 1s orbital: 1s²
Next two electrons fill the 2s orbital: 2s²
The remaining four electrons go into the 2p orbitals. There are three 2p orbitals (px, py, pz). According to Hund's Rule, electrons will individually occupy degenerate orbitals (orbitals of the same energy) before pairing up. So, the first three 2p electrons will go into each of the 2p orbitals with parallel spins. The fourth 2p electron will then pair up in one of the 2p orbitals.
Electron configuration: 1s² 2s² 2p⁴

The chemical properties of elements are directly dictated by their atomic structure, particularly by the configuration of their outermost electrons, known as valence electrons. Elements with similar valence electron configurations tend to exhibit similar chemical properties, which is the basis for the organization of the periodic table. For example, elements in Group 1 (alkali metals) all have a single s electron in their outermost shell (e.g., Li: [He] 2s¹, Na: [Ne] 3s¹). This configuration makes them highly reactive, readily losing that single electron to form a +1 ion. Conversely, elements in Group 17 (halogens) all have seven valence electrons (ns² np⁵) and are highly reactive nonmetals, eager to gain one electron to achieve a stable octet.The historical development of atomic theory is a testament to the scientific method, with each new model building upon previous observations and experiments. From the earliest philosophical musings of Democritus about indivisible particles to the sophisticated quantum mechanical model, our understanding of the atom has continually evolved.

Experimental evidence, such as the cathode ray experiments that led to the discovery of the electron, Rutherford's gold foil experiment that revealed the nucleus, and the analysis of atomic spectra, has been critical in shaping our current understanding.Inorganic chemistry, with its broad scope, demands a foundational understanding of atomic structure.

By mastering concepts like quantum numbers, electron configurations, and the principles governing orbital filling, we gain the tools necessary to predict and explain the chemical behavior of elements and their compounds. This fundamental knowledge is the gateway to exploring more advanced topics in inorganic chemistry, such as bonding theories, coordination chemistry, and solid-state chemistry, ultimately enabling us to design and synthesize new materials with desired properties for a myriad of applications.

Chapter 2: Periodic Trends and Chemical Bonding

Having explored the fundamental building blocks of matter – atoms – and their intricate internal structures, we now embark on a journey to understand how these atoms interact with one another. This interaction dictates the very nature of all substances around us, from the water we drink to the air we breathe and the complex molecules that make up living organisms. Our journey begins by observing recurring patterns, or periodic trends, in the properties of elements, which are directly attributable to their atomic structure. These trends provide a powerful predictive tool for understanding chemical behavior. We will then delve into the fascinating world of chemical bonding, the forces that hold atoms together, exploring the diverse types of bonds and the theories that explain their formation. Finally, we will examine the crucial role of intermolecular forces in shaping the macroscopic properties of matter.

Periodic Trends: Unveiling the Patterns

The periodic table, a masterpiece of chemical organization, is more than just a list of elements; it's a profound statement about the underlying principles governing atomic properties. As we move across periods (rows) and down groups (columns), we observe systematic changes in several key atomic characteristics.

Atomic and Ionic Radii

Atomic radius refers to the typical distance from the nucleus to the outermost electron shell of an atom. Imagine an atom as a tiny sphere; its radius is a measure of its size.

Across a period (left to right): Atomic radius generally decreases. This is because as we move across a period, the number of protons in the nucleus increases, leading to a stronger positive charge. While electrons are added to the same principal energy level, the increased nuclear charge pulls all the electrons closer to the nucleus, effectively shrinking the atom.
- Practical Example: Lithium (Li) has an atomic radius of 152 pm, while Neon (Ne), in the same period, has a radius of 69 pm. The increasing nuclear charge from Li to Ne pulls the electrons in the second shell more tightly.
Down a group (top to bottom): Atomic radius generally increases. As we descend a group, electrons are added to successively higher principal energy levels, which are further away from the nucleus. Even though the nuclear charge also increases, the shielding effect of inner electrons counteracts some of this pull, allowing the outer electrons to occupy larger orbitals.
- Practical Example: Comparing Lithium (Li, 152 pm) to Sodium (Na, 186 pm) and Potassium (K, 227 pm) down Group 1, we see a clear increase in atomic radius as more electron shells are added.

Ionic radius is the radius of an ion. Ions are formed when atoms gain or lose electrons.

Cations (positively charged ions):Cations are smaller than their parent atoms. When an atom loses electrons, the remaining electrons experience a stronger effective nuclear charge, pulling them closer to the nucleus. Additionally, sometimes an entire electron shell is lost.
- Practical Example:A sodium atom (Na) has an atomic radius of 186 pm, but a sodium ion (Na
```
 +^++ 
```
  ) has an ionic radius of 102 pm. It has lost its outermost electron and thus its entire third electron shell.
Anions (negatively charged ions):Anions are larger than their parent atoms. When an atom gains electrons, the increased electron-electron repulsion among the added electrons causes the electron cloud to expand.
- Practical Example:A chlorine atom (Cl) has an atomic radius of 99 pm, but a chloride ion (Cl
```
 −^-− 
```
  ) has an ionic radius of 181 pm due to the added electron and increased repulsion.

Ionization Energy

Ionization energy (IE) is the minimum energy required to remove one electron from a gaseous atom in its ground state, forming a cation. The first ionization energy (IE1) refers to the removal of the first electron, IE2 for the second, and so on.

Across a period: Ionization energy generally increases. This is due to the increasing effective nuclear charge. As the nucleus exerts a stronger pull on the valence electrons, more energy is required to overcome this attraction and remove an electron.
- Practical Example: From Lithium (Li, IE1 = 520 kJ/mol) to Neon (Ne, IE1 = 2081 kJ/mol), the energy required to remove the first electron steadily increases. Neon, being a noble gas with a full valence shell, is very reluctant to lose an electron.
Down a group: Ionization energy generally decreases. As atomic size increases down a group, the outermost electrons are further from the nucleus and are also shielded by more inner electrons. This weaker attraction makes it easier to remove an electron, hence requiring less energy.
- Practical Example: The IE1 of Lithium (Li, 520 kJ/mol) is higher than that of Sodium (Na, 496 kJ/mol) and Potassium (K, 419 kJ/mol).

Electron Affinity

Electron affinity (EA) is the energy change that occurs when an electron is added to a gaseous atom, forming an anion. A more negative (or more exothermic) electron affinity indicates a greater tendency for an atom to gain an electron.

Across a period: Electron affinity generally becomes more negative(more favorable for electron gain). Atoms with smaller sizes and higher effective nuclear charges have a stronger attraction for additional electrons. Halogens (Group 17) have the most negative electron affinities because gaining one electron completes their octet.
- Practical Example: Fluorine (F) has a highly negative EA of -328 kJ/mol, indicating a strong desire to gain an electron and achieve a stable noble gas configuration. In contrast, Beryllium (Be) has a positive EA, meaning energy must be supplied to force it to accept an electron, as it already has a full s-subshell.
Down a group: Electron affinity generally becomes less negative(less favorable for electron gain). As atoms get larger, the incoming electron is further from the nucleus and experiences greater shielding, leading to a weaker attraction.
- Practical Example: Chlorine (Cl, EA = -349 kJ/mol) has a slightly more negative electron affinity than Fluorine (F, EA = -328 kJ/mol), which is an interesting exception due to fluorine's small size leading to significant electron-electron repulsion in the compact 2p subshell when an electron is added. However, subsequent elements like Bromine (Br, -325 kJ/mol) and Iodine (I, -295 kJ/mol) follow the expected trend of decreasing (less negative) electron affinity.

Electronegativity

Electronegativity is a measure of the ability of an atom in a chemical bond to attract shared electrons towards itself. It's not energy but a relative scale, typically represented by the Pauling scale (from 0.7 to 4.0).

Across a period: Electronegativity generally increases. Atoms become smaller, and the effective nuclear charge increases, giving them a stronger pull on shared electrons.
- Practical Example: Oxygen (3.44) is more electronegative than Carbon (2.55) in the same period. This explains why oxygen "pulls" electrons more strongly in bonds like those in water.
Down a group: Electronegativity generally decreases. As atoms get larger, the valence electrons are further from the nucleus and more shielded, resulting in a weaker attraction for shared electrons.
- Practical Example: Fluorine (3.98) is the most electronegative element, while Chlorine (3.16), Bromine (2.96), and Iodine (2.66) show decreasing electronegativity down Group 17.

Chemical Bonding: The Glue That Holds Matter Together

The periodic trends discussed above are direct manifestations of how atoms strive to achieve greater stability, often by attaining a noble gas electron configuration (a full outer shell). This drive for stability is the impetus behind chemical bonding, the fundamental process by which atoms join together. We will explore three primary types of chemical bonds: ionic, covalent, and metallic.

Ionic Bonding

Ionic bonding occurs between a metal and a nonmetal. It involves the complete transfer of one or more electrons from the metal atom (which typically has a low ionization energy and low electronegativity) to the nonmetal atom (which typically has a high electron affinity and high electronegativity). This transfer results in the formation of oppositely charged ions (cations and anions), which are then held together by strong electrostatic forces of attraction.

Practical Example: The formation of sodium chloride (NaCl), common table salt.
- Sodium (Na), a Group 1 metal, readily loses its single valence electron to form a Na
```
 +^++ 
```
  cation (achieving a stable electron configuration like Neon).
- Chlorine (Cl), a Group 17 nonmetal, readily gains one electron to form a Cl
```
 −^-− 
```
  anion (achieving a stable electron configuration like Argon).
- The strong electrostatic attraction between the positively charged Na
```
 +^++ 
```
  and negatively charged Cl
```
 −^-− 
```
  ions forms the ionic bond in NaCl.

Ionic compounds typically form crystalline solids with high melting points, are often soluble in water, and conduct electricity when molten or dissolved because their ions are free to move.

Covalent Bonding

Covalent bonding occurs primarily between two nonmetal atoms. Instead of transferring electrons, atoms share electrons to achieve a stable electron configuration, typically an octet. The shared electrons are mutually attracted to the nuclei of both atoms, holding them together.

Practical Example: The formation of a water molecule (H
```
 2_22 
```
O).
- An oxygen atom (O) has 6 valence electrons and needs 2 more to complete its octet.
- Each hydrogen atom (H) has 1 valence electron and needs 1 more to complete its duet (like Helium).
- Oxygen shares one of its electrons with one hydrogen, and another electron with the second hydrogen. Each hydrogen also shares its electron with oxygen. This results in two single covalent bonds, with oxygen having two lone pairs of electrons.

Covalent compounds can exist as gases, liquids, or solids with generally lower melting points than ionic compounds. They are typically poor conductors of electricity as there are no free-moving charged particles.Valence Bond Theory (VBT) explains covalent bond formation by proposing that atomic orbitals on different atoms overlap to form a shared region of electron density. The greater the overlap, the stronger the bond.

Hybridization: VBT introduces the concept of hybridizationto explain the observed geometries of molecules. When atoms form bonds, their atomic orbitals sometimes mix to form new, equivalent hybrid orbitals that are more suitable for bonding and minimize electron repulsion.
- Practical Example: Methane (CH
```
 4_44 
```
  ). Carbon has one 2s and three 2p orbitals. To form four equivalent bonds with four hydrogen atoms, carbon's 2s and three 2p orbitals hybridize to form four equivalent sp
  3^33
  hybrid orbitals. These sp
```
 3^33 
```
  orbitals point towards the corners of a tetrahedron, giving methane its characteristic tetrahedral geometry (109.5° bond angles).
- Practical Example: Ethylene (C
```
 2_22 
```
  H
  4_44
  ). In ethylene, each carbon undergoes sp
  2^22
  hybridization. One 2s and two 2p orbitals hybridize to form three sp
```
 2^22 
```
  orbitals, which lie in a plane at 120° angles to each other (trigonal planar geometry). The remaining unhybridized 2p orbital on each carbon overlaps sideways to form a pi (π) bond, while the sp
```
 2^22 
```
  orbitals overlap end-to-end to form sigma (σ) bonds. This combination results in a carbon-carbon double bond.
- Practical Example: Acetylene (C
```
 2_22 
```
  H
  2_22
  ). In acetylene, each carbon undergoes sp hybridization. One 2s and one 2p orbital hybridize to form two sp orbitals, which are linear (180° apart). The two remaining unhybridized 2p orbitals on each carbon overlap sideways to form two pi (π) bonds, while the sp orbitals overlap end-to-end to form a sigma (σ) bond. This results in a carbon-carbon triple bond.

Molecular Orbital Theory (MOT) offers a more sophisticated quantum mechanical description of bonding. Instead of atomic orbitals overlapping, MOT proposes that atomic orbitals combine to form new molecular orbitals that extend over the entire molecule. Electrons then occupy these molecular orbitals, just as they occupy atomic orbitals in individual atoms.

Bonding and Antibonding Orbitals:When atomic orbitals combine, they form two types of molecular orbitals:
- Bonding molecular orbitals: Lower in energy than the original atomic orbitals, leading to increased electron density between nuclei and thus stabilization.
- Antibonding molecular orbitals: Higher in energy, with a node (zero electron density) between nuclei, destabilizing the molecule if occupied.
Bond Order: MOT allows for the calculation of bond order, which is (number of electrons in bonding MOs - number of electrons in antibonding MOs) / 2. A bond order of 1 signifies a single bond, 2 a double bond, and so on. A bond order of zero means no stable bond forms.
- Practical Example: Hydrogen (H
```
 2_22 
```
  ). Each hydrogen atom contributes one 1s atomic orbital. These combine to form one σ (sigma) bonding molecular orbital and one σ* (sigma star) antibonding molecular orbital. The two electrons (one from each H) fill the lower-energy σ bonding orbital. Bond order = (2-0)/2 = 1, indicating a stable single bond.
- Practical Example: Helium (He
```
 2_22 
```
  ). Each helium contributes one 1s atomic orbital. These combine to form one σ bonding and one σ* antibonding molecular orbital. The four electrons (two from each He) fill both the σ bonding and the σ* antibonding orbitals. Bond order = (2-2)/2 = 0, correctly predicting that He
```
 2_22 
```
  does not form a stable molecule.

Sometimes, a single Lewis structure cannot adequately describe the true bonding in a molecule because the electrons are delocalized (spread out) over several atoms. In such cases, we use the concept of resonance, where the actual structure is an average or hybrid of two or more contributing resonance structures.

Practical Example: Benzene (C
```
 6_66 
```
H
6_66
). Benzene is a cyclic molecule with alternating single and double bonds in its traditional Lewis structure. However, experimental evidence shows all carbon-carbon bonds are of equal length, intermediate between single and double bonds. Resonance explains this by depicting benzene as a hybrid of two equivalent resonance structures, with the pi electrons delocalized around the ring.

Practical Example: Carbonate Ion (CO
```
 32−_3^{2-}32− 
```
). The carbonate ion has one carbon atom double-bonded to one oxygen and single-bonded to two other oxygens. However, experimentally, all three C-O bonds are found to be identical in length. This is explained by resonance, where the double bond character is delocalized over all three C-O bonds, represented by three contributing resonance structures.

Metallic Bonding

Metallic bonding is found in solid metals and alloys. It involves a "sea" of delocalized valence electrons shared among a lattice of positively charged metal ions. Unlike ionic bonds (localized attraction between specific ions) or covalent bonds (localized shared electron pairs), metallic bonds feature electrons that are not associated with any single atom or bond but are free to move throughout the entire structure.

Practical Example: Copper (Cu). In a piece of copper wire, each copper atom contributes its valence electrons to a collective "sea." These electrons are highly mobile, allowing metals to be excellent conductors of heat and electricity. The strong electrostatic attraction between the positively charged copper ions and the surrounding electron sea gives metals their characteristic properties like malleability (can be hammered into sheets), ductility (can be drawn into wires), and luster.

Intermolecular Forces: Shaping Bulk Properties

While chemical bonds are the strong forces within molecules (intramolecular forces), intermolecular forces (IMFs) are the weaker attractive forces between molecules. These forces are crucial in determining the physical properties of substances, such as melting points, boiling points, viscosity, and solubility.

Types of Intermolecular Forces

London Dispersion Forces (LDFs): These are the weakest IMFs and are present in allmolecules, polar and nonpolar alike. They arise from temporary, instantaneous dipoles that occur due to the random movement of electrons. These temporary dipoles induce temporary dipoles in neighboring molecules, leading to weak, fleeting attractions.
- Practical Example: The noble gases (He, Ne, Ar, Kr, Xe) exist as individual atoms and are nonpolar, so LDFs are their only intermolecular forces. The increasing boiling points down the group (He = -269 °C, Xe = -108 °C) demonstrate that larger atoms with more electrons have stronger LDFs due to increased polarizability (the ease with which their electron cloud can be distorted).
- Practical Example:Nonpolar molecules like methane (CH
```
 4_44 
```
  ) and hexane (C
```
 6_66 
```
  H
```
 14_{14}14 
```
  ) are held together in their liquid and solid states by LDFs. Hexane has a higher boiling point than methane because its larger size and greater number of electrons lead to stronger LDFs.
Dipole-Dipole Forces: These forces occur between polarmolecules. Polar molecules have permanent dipoles due to unequal sharing of electrons within covalent bonds (electronegativity differences), creating partial positive and partial negative ends. The partial positive end of one molecule is attracted to the partial negative end of a neighboring molecule.
- Practical Example:Hydrogen chloride (HCl) is a polar molecule. The partial positive hydrogen of one HCl molecule is attracted to the partial negative chlorine of another HCl molecule. Acetone ((CH
```
 3_33 
```
  )
```
 2_22 
```
  CO) is another example of a molecule with significant dipole-dipole interactions, contributing to its relatively high boiling point compared to nonpolar molecules of similar size.
Hydrogen Bonding:This is a particularly strong type of dipole-dipole interaction. It occurs when hydrogen is covalently bonded to a highly electronegative atom (N, O, or F), and that hydrogen is then attracted to a lone pair of electrons on another highly electronegative atom (N, O, or F) in a neighboring molecule.
- Practical Example: Water (H
```
 2_22 
```
  O)exhibits extensive hydrogen bonding. Each water molecule can form up to four hydrogen bonds with other water molecules. This strong network of hydrogen bonds gives water its unusually high boiling point (100 °C) compared to other hydrides of Group 16 elements like H
```
 2_22 
```
  S (-60 °C), where hydrogen bonding is absent.
- Practical Example: Hydrogen bonding is crucial for the structure of DNA and proteins, holding together the two strands of the DNA double helix and contributing to the intricate folding of protein molecules.

Conclusion

The periodic trends in atomic properties provide a framework for understanding and predicting how elements will behave. These trends culminate in the diverse ways atoms form chemical bonds – ionic, covalent, and metallic – each with distinct characteristics and resulting material properties. Furthermore, the often-overlooked intermolecular forces play a critical role in dictating the bulk physical properties of substances. By understanding these fundamental principles, we gain profound insights into the vast and intricate world of chemistry, laying the groundwork for exploring more complex chemical reactions and structures.

Chapter 3: Molecular Symmetry and Group Theory

Molecular symmetry is a fundamental concept in chemistry that allows us to understand, predict, and explain various molecular properties, including spectroscopy, bonding, and reactivity. By recognizing the symmetry elements present in a molecule and classifying them into point groups, we gain a powerful tool for simplifying complex chemical problems. This chapter will delve into the core principles of molecular symmetry and introduce the fascinating world of group theory, a mathematical framework that underpins these concepts.

Symmetry Elements and Operations

At the heart of molecular symmetry are symmetry elements, which are geometric entities (points, lines, or planes) that define the location of symmetry operations. A symmetry operation is a movement of a molecule such that, after the operation, the molecule is indistinguishable from its original orientation. Let's explore the five fundamental types of symmetry elements and their corresponding operations:

Identity (E): The simplest symmetry element is the entire molecule itself. The corresponding operation, the identity operation (E), involves doing nothing to the molecule. Every molecule possesses the identity element, as it always looks the same to itself. While seemingly trivial, it's crucial for the mathematical framework of group theory.
Rotation Axis (Cn): A rotation axis (Cn) is an imaginary line passing through the molecule. The corresponding operation, a proper rotation (Cn), involves rotating the molecule by 360°/n around this axis. If, after the rotation, the molecule appears identical, then a Cn axis exists. The integer 'n' indicates the order of the axis.
- Example: Water (H2O)
  Water has a C2 rotation axis passing through the oxygen atom and bisecting the H-O-H angle. If you rotate the water molecule by 180° (360°/2) around this axis, the two hydrogen atoms exchange positions, but the molecule looks exactly the same.
- Example: Ammonia (NH3)
  Ammonia possesses a C3 rotation axis passing through the nitrogen atom and perpendicular to the plane formed by the hydrogen atoms. A 120° rotation around this axis interchanges the three hydrogen atoms, resulting in an indistinguishable molecule.
- Example: Benzene (C6H6)
  Benzene is a classic example with a C6 rotation axis perpendicular to the ring plane and passing through the center of the ring. A 60° rotation (360°/6) leaves the molecule unchanged. Benzene also has three C2 axes passing through opposite carbon atoms and three C2 axes passing through the midpoints of opposite C-C bonds.
Mirror Plane (σ): A mirror plane (σ) is an imaginary plane that bisects the molecule. The corresponding operation, reflection (σ), involves reflecting all atoms through this plane. If the reflected molecule is identical to the original, a mirror plane exists. There are three types of mirror planes:
- Vertical Mirror Plane (σv):Contains the principal rotation axis (the Cn axis with the highest order).
  - Example: Water (H2O)
    Water has two σv planes. One contains the C2 axis and the two O-H bonds. The other also contains the C2 axis but bisects the H-O-H angle, essentially passing between the two hydrogen atoms.
- Horizontal Mirror Plane (σh):Perpendicular to the principal rotation axis.
  - Example: Boron Trifluoride (BF3)
    BF3 is trigonal planar. It has a C3 axis passing through the boron atom. Perpendicular to this C3 axis is a σh plane that contains all the atoms of the molecule.
- Dihedral Mirror Plane (σd):Bisects the angle between two C2 axes perpendicular to the principal axis. They also contain the principal axis.
  - Example: Ethane (staggered conformation)
    Staggered ethane has a C3 principal axis. It also has three C2 axes perpendicular to the C3 axis. Between these C2 axes lie three σd planes.
Inversion Center (i): An inversion center (i) is a point within the molecule. The corresponding operation, inversion (i), involves taking every atom in the molecule, drawing a line from that atom through the inversion center, and extending the line an equal distance on the other side. If an identical atom is found at that new position, an inversion center exists.
- Example: Benzene (C6H6)
  The center of the benzene ring is an inversion center. If you take any carbon atom, draw a line through the center, and extend it, you'll find an identical carbon atom. The same applies to hydrogen atoms.
- Example: trans-1,2-Dichloroethene
  This molecule has an inversion center at the midpoint of the C=C bond.
Improper Rotation Axis (Sn): An improper rotation axis (Sn) is a combination of two operations: a proper rotation (Cn) followed by a reflection through a plane perpendicular to the Cn axis (σh). The corresponding operation is an improper rotation (Sn).
- Example: Methane (CH4)
  Methane has three S4 axes. Consider an S4 axis passing through the carbon atom and two opposite hydrogen atoms. A 90° rotation (C4) followed by a reflection through a plane perpendicular to this C4 axis (σh) results in an indistinguishable molecule.

Point Groups

Molecules are classified into point groups based on the specific combination of symmetry elements they possess. A point group is a collection of all symmetry operations that can be performed on a molecule that leave at least one point in the molecule fixed. There are flowcharts and tables to systematically assign point groups, but here are some common examples:

C1: Only the identity element (E). Asymmetric molecules (e.g., CHFClBr).
Cs: E and a mirror plane (σ). (e.g., H2CCl2, the plane bisects the Cl-C-Cl and H-C-H angles).
Ci: E and an inversion center (i). (e.g., trans-1,2-dichloro-1,2-dibromoethane in certain conformations).
Cn: E and a Cn axis. (e.g., H2O2 in a specific conformation, though it's often C2).
Cnv: E, a Cn axis, and n vertical mirror planes (σv). (e.g., H2O (C2v), NH3 (C3v)).
Cnh: E, a Cn axis, and a horizontal mirror plane (σh). (e.g., trans-N2F2 (C2h)).
Dn: E, a Cn axis, and n C2 axes perpendicular to Cn. (e.g., biphenyl in its D2 conformation).
Dnh: E, a Cn axis, n C2 axes perpendicular to Cn, and a horizontal mirror plane (σh). This is a very common and important group. (e.g., Benzene (D6h), BF3 (D3h), Ethylene (D2h)).
Dnd: E, a Cn axis, n C2 axes perpendicular to Cn, and n dihedral mirror planes (σd). (e.g., Ethane (staggered, D3d)).
Sn: E and an Sn axis (where n is even). These are less common for simple molecules.
Td: Tetrahedral symmetry (e.g., CH4). Possesses multiple C3 axes, C2 axes, and S4 axes.
Oh: Octahedral symmetry (e.g., SF6). Possesses multiple C4, C3, C2 axes, and an inversion center.
Ih: Icosahedral symmetry (e.g., C60 fullerene). High symmetry with many C5 axes.
R∞h: Linear molecules with an inversion center (e.g., CO2, H2).
C∞v: Linear molecules without an inversion center (e.g., HCl, CO).

Assigning a point group is a systematic process. One typically starts by looking for the highest order rotation axis (the principal axis), then checks for perpendicular C2 axes, then for a horizontal mirror plane, and so on.

Basics of Group Theory

Group theory provides the mathematical framework for understanding symmetry. A group in mathematics is a set of elements (in our case, symmetry operations) together with a binary operation (sequential application of operations) that satisfies four specific conditions:

Closure: The product of any two operations in the group must also be an operation within the group.
Associativity: (AB)C = A(BC), where A, B, and C are operations.
Identity Element: There is an identity operation (E) such that EA = AE = A for all A in the group.
Inverse Element: For every operation A in the group, there is an inverse operation A⁻¹ such that AA⁻¹ = A⁻¹A = E.

Character Tables and Irreducible Representations

One of the most powerful tools derived from group theory in chemistry is the character table. A character table summarizes the symmetry properties of a point group. Each row in a character table corresponds to an irreducible representation (Γ), which describes how molecular properties (like atomic orbitals, vibrations, or electronic states) transform under the symmetry operations of the group. Each column represents a symmetry operation or a class of symmetry operations. The entries in the table, called characters, are numbers that indicate how a particular irreducible representation behaves under a specific symmetry operation.Let's look at the C2v point group character table (for water):

C2v	E	C2	σv(xz)	σv'(yz)
A1	1	1	1	1	z	x², y², z²
A2	1	1	-1	-1	Rz	xy
B1	1	-1	1	-1	x, Ry	xz
B2	1	-1	-1	1	y, Rx	yz

Rows (Irreducible Representations): A1, A2, B1, B2. These are standard labels. 'A' denotes representations that are symmetric (character = 1) with respect to rotation about the principal axis, 'B' denotes antisymmetric (character = -1). Subscripts 1 and 2 distinguish representations further.
Columns (Symmetry Operations): E (identity), C2 (rotation), σv(xz) (mirror plane containing xz plane), σv'(yz) (mirror plane containing yz plane).
Characters: The numbers (1, -1) indicate how a function belonging to that representation transforms. For example, a function belonging to A1 remains unchanged (character = 1) under all operations. A function belonging to B2 changes sign (character = -1) under C2 and σv(xz), but remains unchanged under σv'(yz).
Rightmost Columns (Basis Functions): These columns show which common functions (like x, y, z coordinates, rotations Rx, Ry, Rz, and quadratic functions like x², xy, etc.) belong to each irreducible representation. This is crucial for applications. For example, the z-axis transforms as A1, meaning an orbital pointing along the z-axis (like a pz orbital) has A1 symmetry.

Applications of Symmetry

Group theory and molecular symmetry have profound implications across various fields of chemistry:

Spectroscopy:Symmetry rules govern whether a particular transition (e.g., electronic, vibrational, rotational) is allowed or forbidden in various spectroscopic techniques (IR, Raman, UV-Vis, NMR).
- Infrared (IR) Spectroscopy: For a vibrational mode to be IR active, it must induce a change in the molecule's dipole moment. Group theory allows us to determine which vibrational modes have the necessary symmetry to be IR active. For water (C2v), the symmetric stretch, asymmetric stretch, and bending modes are all IR active because they belong to A1 or B1 representations, which correspond to changes in dipole moment along the x, y, or z axes.
- Raman Spectroscopy: For a vibrational mode to be Raman active, it must induce a change in the molecule's polarizability. Again, group theory helps identify these modes.
Bonding and Molecular Orbital Theory:Symmetry considerations are fundamental in constructing molecular orbital diagrams. Atomic orbitals of the correct symmetry can combine to form molecular orbitals.
- Example: Water (H2O)
  The atomic orbitals of oxygen (2s, 2px, 2py, 2pz) and the combination of hydrogen 1s orbitals (symmetric and antisymmetric combinations) are assigned to irreducible representations of the C2v point group. Only atomic orbitals or symmetry-adapted linear combinations of atomic orbitals (SALCs) belonging to the same irreducible representation can combine to form molecular orbitals. This significantly simplifies the molecular orbital construction and helps explain the bonding in water.
Reaction Mechanisms: Symmetry can predict the allowedness of certain reaction pathways, especially in pericyclic reactions (e.g., Woodward-Hoffmann rules).
Chirality: Molecules lacking any Sn axis (including S1=σ and S2=i) are chiral. This provides a rigorous definition of chirality, which is crucial in stereochemistry and pharmaceutical chemistry.
Crystal Field and Ligand Field Theory: In coordination chemistry, the splitting of d-orbitals in transition metal complexes is dictated by the symmetry of the ligand environment. Group theory is used to determine the irreducible representations of the d-orbitals in different geometries.

In conclusion, molecular symmetry and group theory provide an elegant and powerful framework for understanding molecular structure and properties. By systematically identifying symmetry elements and classifying molecules into point groups, chemists gain invaluable insights into spectroscopic behavior, bonding patterns, and reactivity, simplifying otherwise complex problems.

Chapter 4: Acid-Base Chemistry in Inorganic Systems

Acid-base chemistry is a fundamental concept in all branches of chemistry, including inorganic systems. While often first encountered in the context of aqueous solutions and proton transfer, the definition of acids and bases significantly broadens when considering the vast landscape of inorganic compounds and reactions. This chapter will delve into these expanded definitions, moving beyond the familiar Brønsted-Lowry concept to explore more generalized theories, culminating in the highly practical Hard and Soft Acids and Bases (HSAB) theory. We will illustrate these concepts with numerous practical examples relevant to inorganic synthesis and understanding reactivity.

1. Review of Traditional Acid-Base Theories

1.1 Brønsted-Lowry Theory

The Brønsted-Lowry theory, introduced independently by Johannes Brønsted and Thomas Lowry in 1923, defines an acid as a proton (H+) donor and a base as a proton acceptor. This theory is particularly useful for reactions occurring in protic solvents (solvents that can donate or accept protons, like water or ammonia).

Acid-Base Reaction: Acid + Base ⇌ Conjugate Base + Conjugate AcidExample 1: Aqueous Solution

When hydrogen chloride gas dissolves in water, HCl acts as a Brønsted acid, donating a proton to water, which acts as a Brønsted base.HCl(aq) + H₂O(l) ⇌ Cl⁻(aq) + H₃O⁺(aq)Here, Cl⁻ is the conjugate base of HCl, and H₃O⁺ (hydronium ion) is the conjugate acid of H₂O.

Example 2: Non-Aqueous Brønsted-Lowry

In liquid ammonia, ammonium chloride (NH₄Cl) acts as an acid, donating a proton to ammonia, which acts as a base.NH₄Cl(am) + NH₃(l) ⇌ Cl⁻(am) + NH₄⁺(am)This theory elegantly explains many reactions but is limited to systems involving proton transfer.

1.2 Lewis Acid-Base Theory

Introduced by Gilbert N. Lewis in 1923, the Lewis theory offers a broader definition. A Lewis acid is an electron pair acceptor, and a Lewis base is an electron pair donor. This theory is extremely powerful as it does not require the presence of protons and can describe a wider range of reactions, including coordination complex formation.

Lewis Acid-Base Adduct Formation: A + :B → A-B (adduct)Example 3: Boron Trifluoride and Ammonia

Boron trifluoride (BF₃) has an incomplete octet on boron, making it electron deficient and thus a Lewis acid. Ammonia (NH₃) has a lone pair of electrons on nitrogen, making it an electron pair donor or a Lewis base.BF₃ + :NH₃ → F₃B←NH₃ (boron trifluoride-ammonia adduct)

Here, a new covalent bond is formed where both electrons come from the Lewis base.

Example 4: Metal Ions as Lewis Acids

Transition metal ions are classic Lewis acids, accepting electron pairs from ligands (Lewis bases) to form coordination complexes.Cu²⁺(aq) + 4:NH₃(aq) → [Cu(NH₃)₄]²⁺(aq)

The copper(II) ion (Cu²⁺) acts as a Lewis acid, accepting electron pairs from the ammonia molecules (Lewis bases) to form the tetraamminecopper(II) complex.The Lewis theory is fundamental to understanding coordination chemistry and many inorganic reaction mechanisms.

2. Expanded Acid-Base Concepts for Inorganic Systems

Beyond Brønsted-Lowry and Lewis, several other theories provide useful frameworks for specific inorganic contexts.

2.1 Lux-Flood Theory

Proposed by Hermann Lux (1939) and Håkon Flood (1947), this theory is specifically applicable to high-temperature non-aqueous systems, particularly molten salts and oxides, often encountered in metallurgy and glass manufacturing.A Lux-Flood acid is an oxide ion (O²⁻) acceptor.

A Lux-Flood base is an oxide ion (O²⁻) donor.

Example 5: Reaction of CaO and SiO₂ in a Blast Furnace

In a blast furnace, calcium oxide (CaO) acts as a Lux-Flood base, donating oxide ions, while silicon dioxide (SiO₂) acts as a Lux-Flood acid, accepting oxide ions to form silicate slag.CaO (base) → Ca²⁺ + O²⁻

SiO₂ (acid) + O²⁻ → SiO₃²⁻Overall: CaO + SiO₂ → CaSiO₃ (calcium silicate slag)

This reaction is crucial for removing impurities (like silica) from iron ore.

2.2 Usanovich Theory

The most general acid-base theory, proposed by Mikhail Usanovich in 1939, encompasses all other theories.An Usanovich acid is any species that accepts anions or donates cations (including protons) or accepts electrons.

An Usanovich base is any species that donates anions or accepts cations or donates electrons.This theory includes redox reactions and emphasizes the transfer of particles or electrons rather than specific species like protons or electron pairs. While comprehensive, its broadness can sometimes make it less practical for everyday predictions compared to more specific theories.Example 6: Usanovich in a Redox Reaction

Consider the reaction: 2Na + Cl₂ → 2NaCl

Sodium (Na) donates electrons, thus acting as an Usanovich base. Chlorine (Cl₂) accepts electrons, thus acting as an Usanovich acid.

2.3 Solvent System Theory

This theory defines acids and bases relative to the autoionization of the solvent.An acid is a substance that increases the concentration of the characteristic cation of the solvent.

A base is a substance that increases the concentration of the characteristic anion of the solvent.

Example 7: Liquid Ammonia as a Solvent

Liquid ammonia undergoes autoionization: 2NH₃ ⇌ NH₄⁺ (ammonium) + NH₂⁻ (amide)

Acids in liquid ammonia: Substances that produce NH₄⁺. For example, NH₄Cl (ammonium chloride) is an acid because it dissociates to give NH₄⁺ ions.
NH₄Cl → NH₄⁺ + Cl⁻
Bases in liquid ammonia: Substances that produce NH₂⁻. For example, KNH₂ (potassium amide) is a base because it dissociates to give NH₂⁻ ions.
KNH₂ → K⁺ + NH₂⁻

Example 8: Liquid Sulfur Dioxide as a Solvent

Liquid SO₂ undergoes autoionization: 2SO₂ ⇌ SO²⁺ (thionyl ion) + SO₃²⁻ (sulfite ion)

Acids in liquid SO₂: Substances that produce SO²⁺. For example, SOCl₂ (thionyl chloride) is an acid.
SOCl₂ → SO²⁺ + 2Cl⁻
Bases in liquid SO₂: Substances that produce SO₃²⁻. For example, Cs₂SO₃ (cesium sulfite) is a base.
Cs₂SO₃ → 2Cs⁺ + SO₃²⁻

This theory is crucial for understanding reactions and solubilities in non-aqueous solvents, which are often employed in inorganic synthesis to achieve unique reaction pathways or stabilize reactive intermediates.

3. Hard and Soft Acids and Bases (HSAB) Theory

Developed by Ralph Pearson in the 1960s, the Hard and Soft Acids and Bases (HSAB) theory is an extension of the Lewis acid-base concept and provides an invaluable qualitative framework for predicting the stability of complexes and the outcomes of displacement reactions, particularly in inorganic chemistry.The central tenet of HSAB is: "Hard acids prefer to bind to hard bases, and soft acids prefer to bind to soft bases."

3.1 Definitions of Hard and Soft

Hard Species:

Small size
High charge density (for acids)
High electronegativity (for bases)
Low polarizability (electron cloud is not easily distorted)
Involved in primarily ionic bonding.
Examples of Hard Acids: H⁺, Li⁺, Na⁺, K⁺, Mg²⁺, Ca²⁺, Al³⁺, Cr³⁺, Fe³⁺, Co³⁺, Ti⁴⁺, BF₃, AlCl₃, SO₃.
Examples of Hard Bases: F⁻, Cl⁻, OH⁻, O²⁻, NH₃, H₂O, CO₃²⁻, SO₄²⁻, PO₄³⁻.

Soft Species:

Large size
Low charge density (for acids)
Low electronegativity (for bases)
High polarizability (electron cloud is easily distorted)
Involved in primarily covalent bonding.
Examples of Soft Acids: Cu⁺, Ag⁺, Au⁺, Hg²⁺, Cd²⁺, Pt²⁺, Pd²⁺, BH₃, I₂, SO₂.
Examples of Soft Bases: H⁻, I⁻, S²⁻, CN⁻, CO, R₃P (phosphines), C₂H₄ (alkenes), benzene.

Borderline Species:

Some acids and bases exhibit intermediate characteristics.

Borderline Acids: Fe²⁺, Co²⁺, Ni²⁺, Cu²⁺, Zn²⁺, Pb²⁺, SO₂.
Borderline Bases: Br⁻, NO₂⁻, N₂, pyridine, aniline.

3.2 Principles and Applications of HSAB Theory

1. Predicting Stability of Complexes:

HSAB theory predicts that complexes formed between a hard acid and a hard base (HA-HB) or a soft acid and a soft base (SA-SB) will be more stable than those formed between a hard acid and a soft base (HA-SB) or a soft acid and a hard base (SA-HB).

Example 9: Stability of Silver Halides

Ag⁺ is a soft acid.

F⁻ is a hard base.

Cl⁻, Br⁻ are borderline bases.

I⁻ is a soft base.

According to HSAB, the stability of silver halides should increase as the base becomes softer: AgF < AgCl < AgBr < AgI.

Indeed, AgI is the most stable and least soluble silver halide, reflecting the strong soft-soft interaction.

Example 10: Preferential Binding of CN⁻ and F⁻ to Fe²⁺ and Fe³⁺

Fe³⁺ (smaller, higher charge) is a harder acid than Fe²⁺ (larger, lower charge).

CN⁻ is a soft base (large, polarizable, good sigma donor and pi acceptor).

F⁻ is a hard base (small, high electronegativity).

Therefore, Fe³⁺ will preferentially bind to F⁻ (hard-hard interaction), while Fe²⁺ will show a stronger preference for CN⁻ (soft-soft interaction). This explains why [FeF₆]³⁻ is more stable than [Fe(CN)₆]³⁻, and [Fe(CN)₆]⁴⁻ is more stable than [FeF₆]⁴⁻.

2. Predicting Reaction Outcomes (Displacement Reactions):

HSAB theory can predict which way a reaction will proceed based on the principle of forming more stable hard-hard or soft-soft combinations.

Example 11: Mercury(II) Sulfide vs. Mercury(II) Oxide

Consider the reaction: HgO + H₂S ⇌ HgS + H₂O

Hg²⁺ is a soft acid.

O²⁻ is a hard base.

S²⁻ is a soft base.

H⁺ (in H₂S/H₂O context) is a hard acid.

Reactants: Hg²⁺-O²⁻ (soft-hard, unstable) and H⁺-S²⁻ (hard-soft, unstable).
Products: Hg²⁺-S²⁻ (soft-soft, stable) and H⁺-O²⁻ (hard-hard, stable).

The reaction will proceed to the right, forming the more stable hard-hard (H₂O) and soft-soft (HgS) combinations. This explains why mercuric sulfide (cinnabar) is found naturally, not mercuric oxide.

Example 12: Complexation of Cd²⁺ with Halides

Cd²⁺ is a borderline acid, but leans towards soft.

F⁻ (hard base), Cl⁻ (borderline), Br⁻ (borderline), I⁻ (soft base).

We would expect Cd²⁺ to form more stable complexes with the softer halides.

Indeed, the stability constants for [CdX₄]²⁻ complexes follow the trend: F⁻ < Cl⁻ < Br⁻ < I⁻. This indicates a stronger interaction with the softer iodide ion.

3. Explaining Reaction Mechanisms:

HSAB can rationalize reaction pathways. For instance, in electrophilic aromatic substitution, the electrophile (an acid) attacks an electron-rich aromatic ring (a base). If the electrophile is soft, it will prefer to attack positions where the electron density is more "soft" or polarizable.4. Applications in Inorganic Synthesis:

Controlling Product Formation: By choosing appropriate hard or soft reagents, chemists can direct reactions towards desired products.
Separation Chemistry: HSAB helps in designing separation processes, such as extracting specific metal ions from mixtures using ligands that selectively bind to hard or soft metals. For example, soft ligands like thiols or phosphines are used to extract soft metal ions like Hg²⁺ or Ag⁺ from aqueous solutions.
Catalysis: Understanding the hard-soft nature of metal centers and ligands is crucial in designing catalysts, as it influences the binding of substrates and the stability of intermediates.

Conclusion

The journey through acid-base theories in inorganic systems reveals a fascinating expansion of fundamental concepts. From the proton-centric Brønsted-Lowry to the electron pair focus of Lewis, and then to the specialized contexts of Lux-Flood and solvent systems, each theory offers a unique lens through which to understand chemical reactivity. The pinnacle of this exploration, the Hard and Soft Acids and Bases (HSAB) theory, provides a powerful and intuitive predictive tool for inorganic chemists. By appreciating the hard-soft characteristics of various species, we can predict the stability of coordination complexes, the direction of chemical reactions, and design strategies for inorganic synthesis and separation, underscoring the profound utility of these acid-base concepts in the inorganic world.`

Chapter 5: Chemistry of Main Group Elements I (Groups 1, 2, 13, 14)

Welcome to the fascinating world of main group elements, the building blocks of countless compounds that shape our everyday lives and the natural world. This chapter embarks on a detailed exploration of the first four main groups, unraveling their characteristic properties, reactivity, and the intriguing chemistry of their most prominent members. We'll start with the highly reactive metallic groups, Group 1 and Group 2, before delving into the more diverse chemistries of Groups 13 and 14, where metallic, metalloid, and non-metallic behaviors converge.

Group 1: The Alkali Metals (Li, Na, K, Rb, Cs, Fr)

The alkali metals, comprising lithium (Li), sodium (Na), potassium (K), rubidium (Rb), cesium (Cs), and francium (Fr), are perhaps the most quintessential metals. Characterized by a single valence electron in their outermost s orbital, they are exceptionally eager to lose this electron to achieve a stable noble gas configuration, forming +1 cations. This strong tendency to donate electrons makes them incredibly reactive and powerful reducing agents.

Trends in Properties:

Atomic Radius: Increases down the group. As more electron shells are added, the valence electron is further from the nucleus.
Ionization Energy: Decreases down the group. The increasing atomic radius and shielding effects make it easier to remove the outermost electron.
Electronegativity: Decreases down the group, reflecting their diminishing attraction for electrons.
Melting and Boiling Points: Decrease down the group. The metallic bonding weakens as the atomic size increases, leading to lower lattice energies. Lithium, for instance, has a melting point of 180.5 °C, while cesium melts at a mere 28.5 °C, making it a liquid near room temperature.
Density: Generally increases down the group, though potassium is less dense than sodium due to its unusually large atomic volume relative to its mass.
Reactivity: Increases dramatically down the group. This is due to the decreasing ionization energy, making it progressively easier to lose that single valence electron.

Characteristic Reactions:

Reaction with Water:Alkali metals react vigorously, often explosively, with water to produce hydrogen gas and a metal hydroxide. The reaction becomes more intense down the group.
- Example: Sodium metal, when dropped into water, melts into a sphere and darts across the surface, fizzing vigorously as hydrogen gas is produced, often igniting with a characteristic orange flame.
  2Na(s) + 2H₂O(l) → 2NaOH(aq) + H₂(g)
- Potassium's reaction is even more violent, often igniting with a lilac flame. Cesium reacts explosively, shattering its container.
Reaction with Halogens:They readily combine with halogens (Group 17) to form ionic halides.
- Example: Sodium burns brightly in chlorine gas to form sodium chloride (table salt).
  2Na(s) + Cl₂(g) → 2NaCl(s)
Reaction with Oxygen:Alkali metals react with oxygen in various ways depending on the metal and conditions. Lithium forms a normal oxide (Li₂O), sodium forms a peroxide (Na₂O₂), and potassium, rubidium, and cesium primarily form superoxides (KO₂, RbO₂, CsO₂).
- Example: When sodium is burned in excess oxygen, a yellow solid, sodium peroxide, is formed.
  2Na(s) + O₂(g) → Na₂O₂(s)
Reaction with Acids:Highly reactive, they react violently with acids, producing hydrogen gas and a salt.
- Example: Lithium reacts with hydrochloric acid.
  2Li(s) + 2HCl(aq) → 2LiCl(aq) + H₂(g)

Common Compounds:Alkali metals form a vast array of ionic compounds, most of which are soluble in water. Examples include:

Sodium chloride (NaCl): Common table salt.
Potassium nitrate (KNO₃): Used in fertilizers and gunpowder.
Lithium carbonate (Li₂CO₃): Used in psychiatric medication for bipolar disorder.
Sodium hydroxide (NaOH): Caustic soda, a strong base used in industrial processes.

Group 2: The Alkaline Earth Metals (Be, Mg, Ca, Sr, Ba, Ra)

The alkaline earth metals—beryllium (Be), magnesium (Mg), calcium (Ca), strontium (Sr), barium (Ba), and radium (Ra)—possess two valence electrons in their outermost s orbital. Like alkali metals, they readily lose these electrons to form +2 cations, making them strong reducing agents, though generally less reactive than their Group 1 counterparts.

Trends in Properties:

Atomic Radius: Increases down the group.
Ionization Energy: Decreases down the group. However, their first ionization energy is higher than that of Group 1 elements in the same period, due to a greater nuclear charge and smaller atomic radius.
Electronegativity: Decreases down the group.
Melting and Boiling Points: Show less consistent trends than Group 1, but generally higher than alkali metals due to stronger metallic bonding (two valence electrons contribute to the electron sea).
Density: Generally increases down the group.
Reactivity: Increases down the group, as the two valence electrons become easier to remove.

Characteristic Reactions:

Reaction with Water:
- Beryllium does not react with water or steam.
- Magnesium reacts very slowly with cold water but more readily with steam to form magnesium hydroxide and hydrogen gas.
  Mg(s) + 2H₂O(l) → Mg(OH)₂(s) + H₂(g) (with cold water)
  Mg(s) + H₂O(g) → MgO(s) + H₂(g) (with steam)
- Calcium, strontium, and barium react with cold water, producing hydrogen gas and metal hydroxides, with increasing vigor down the group.
  Ca(s) + 2H₂O(l) → Ca(OH)₂(aq) + H₂(g)
Reaction with Halogens:They react to form ionic dihalides (e.g., MgCl₂, CaF₂).
- Example: Magnesium ribbon burns in chlorine gas.
  Mg(s) + Cl₂(g) → MgCl₂(s)
Reaction with Oxygen:They react with oxygen to form oxides (MO). Barium can also form a peroxide (BaO₂).
- Example: Magnesium burns with a dazzling white flame in air to produce magnesium oxide.
  2Mg(s) + O₂(g) → 2MgO(s)
Reaction with Acids:React vigorously with acids, releasing hydrogen gas.
- Example: Calcium reacting with dilute hydrochloric acid.
  Ca(s) + 2HCl(aq) → CaCl₂(aq) + H₂(g)

Common Compounds:

Calcium carbonate (CaCO₃): Limestone, marble, chalk; essential for shells and bones.
Magnesium hydroxide (Mg(OH)₂): Milk of magnesia, an antacid.
Calcium sulfate (CaSO₄·½H₂O): Plaster of Paris.
Beryllium oxide (BeO): Used in ceramics due to its high melting point and thermal conductivity.

Group 13: The Boron Group (B, Al, Ga, In, Tl)

Group 13 presents a fascinating transition from non-metallic to metallic character. Boron (B) is a metalloid, exhibiting properties of both metals and non-metals, while aluminum (Al), gallium (Ga), indium (In), and thallium (Tl) are metals. They typically form compounds in the +3 oxidation state, reflecting the loss of their three valence electrons (one s and two p electrons).

Trends in Properties:

Atomic Radius: Increases down the group, but gallium's radius is slightly smaller than aluminum's due to poor shielding by the 3d electrons in gallium.
Ionization Energy: Decreases down the group, but irregularities exist due to the d-block contraction.
Electronegativity: Boron is relatively electronegative; metallic character increases down the group.
Metallic Character: Increases down the group. Boron is a semiconductor, while the others are good electrical conductors.

Unique Chemistry of Boron:Boron stands out due to its small size and relatively high electronegativity. It rarely forms simple B³⁺ ions; instead, its chemistry is dominated by covalent bonding. A key feature of boron chemistry is its electron deficiency—it has only three valence electrons for four bonding orbitals, leading to compounds with "three-center two-electron" bonds and unusual structures.

Boranes:These are compounds of boron and hydrogen, famously known for their complex, cage-like structures. The simplest borane is diborane (B₂H₆).
- Example: Diborane (B₂H₆)
  Diborane (B₂H₆) is a dimeric molecule. Each boron atom is bonded to two terminal hydrogen atoms and two bridging hydrogen atoms. The bridging hydrogens form "banana bonds" or three-center two-electron bonds, where two electrons are shared among three atoms (two boron atoms and one hydrogen atom). This unique bonding allows boron to achieve an octet despite having only six valence electrons if considering only two-center two-electron bonds.
- Boranes are important precursors in organic synthesis and have been explored as high-energy fuels.
Boron Trihalides (BF₃, BCl₃, BBr₃, BI₃): These are strong Lewis acids, readily accepting electron pairs due to boron's empty porbital.
- Example: Boron trifluoride (BF₃) reacts with ammonia (NH₃) to form an adduct.
  BF₃ + NH₃ → F₃B-NH₃
  Here, the lone pair on the nitrogen atom of ammonia is donated to the empty orbital on boron.

Chemistry of Aluminum:Aluminum is the most abundant metal in the Earth's crust. It is a silvery-white, lightweight metal, highly resistant to corrosion due to the formation of a thin, self-protecting oxide layer (Al₂O₃).

Amphoteric Nature:Aluminum oxide and hydroxide are amphoteric, meaning they can react with both acids and bases.
- Example: Aluminum hydroxide reacting with an acid and a base.
  Al(OH)₃(s) + 3H⁺(aq) → Al³⁺(aq) + 3H₂O(l)
  Al(OH)₃(s) + OH⁻(aq) → [Al(OH)₄]⁻(aq)
Reactions:Aluminum reacts with oxygen, halogens, and acids, often less vigorously than Group 1 and 2 metals due to its oxide layer.
- Example: The thermite reaction, where powdered aluminum reduces iron(III) oxide with extreme heat.
  2Al(s) + Fe₂O₃(s) → Al₂O₃(s) + 2Fe(l)

Group 14: The Carbon Group (C, Si, Ge, Sn, Pb)

Group 14 is incredibly diverse, encompassing the non-metal carbon (C), the metalloids silicon (Si) and germanium (Ge), and the metals tin (Sn) and lead (Pb). The ability to form four bonds (by sharing their four valence electrons) and catenation (forming long chains of identical atoms) are hallmarks of this group, especially for carbon and silicon.

Trends in Properties:

Atomic Radius: Increases down the group.
Ionization Energy: Decreases down the group, but with irregularities.
Electronegativity: Decreases down the group.
Metallic Character: Increases down the group. Carbon is a non-metal, silicon and germanium are semiconductors, and tin and lead are metals.
Oxidation States: Can exhibit +2 and +4 oxidation states. The stability of the +2 oxidation state increases down the group (inert pair effect), becoming most prominent for lead (Pb²⁺).

Allotropes and Diverse Compounds of Carbon:Carbon's unique ability to form strong covalent bonds with itself and other elements, coupled with its small size, leads to an astonishing variety of allotropes and compounds.

Allotropes of Carbon:
- Diamond: A giant covalent network structure where each carbon atom is sp³ hybridized and tetrahedrally bonded to four other carbon atoms. Extremely hard and an electrical insulator.
- Graphite: Carbon atoms are sp² hybridized and arranged in hexagonal layers. Within layers, strong covalent bonds exist, but between layers, weak Van der Waals forces allow layers to slide, making it soft and a good lubricant. It's also an electrical conductor due to delocalized electrons.
- Fullerenes: Spherical (like buckyballs, C₆₀) or cylindrical (carbon nanotubes) cage-like structures of carbon atoms.
- Graphene: A single layer of graphite, a two-dimensional material with exceptional strength and conductivity.
Organic Chemistry:The vast field of organic chemistry is built upon carbon's ability to form stable chains and rings with hydrogen, oxygen, nitrogen, and other elements.
- Example: Hydrocarbons such as methane (CH₄), ethane (C₂H₆), benzene (C₆H₆) are fundamental to fuels and petrochemicals.
Inorganic Carbon Compounds:
- Carbon Dioxide (CO₂): A greenhouse gas, vital for photosynthesis.
- Carbon Monoxide (CO): A poisonous gas, formed by incomplete combustion.
- Carbonates (e.g., CaCO₃): Important in geological cycles and materials.
- Carbides (e.g., SiC, CaC₂): Hard materials, some used as abrasives.

Chemistry of Silicon:Silicon is the second most abundant element in the Earth's crust, almost always found combined with oxygen in silicates and silica. Its chemistry shares some similarities with carbon but also has significant differences.

Silicon Dioxide (SiO₂): Known as silica, the main component of sand and quartz. Unlike CO₂, which is a discrete molecular gas, SiO₂ forms a giant covalent network structure (similar to diamond), making it a high-melting solid.
Silicates:The backbone of geological minerals. Silicon atoms are tetrahedrally bonded to four oxygen atoms, forming [SiO₄]⁴⁻ units that can link together in chains, rings, sheets, and 3D networks.
- Example: Feldspar, mica, and asbestos are common silicate minerals.
Silicones:Synthetic polymers containing silicon-oxygen backbones with organic groups attached to the silicon atoms. They are known for their high thermal stability, water repellency, and flexibility, used in sealants, lubricants, and medical implants.
- Example: Dimethylpolysiloxane is a common silicone polymer.
Semiconductor Properties: Silicon's metalloid nature makes it crucial in the electronics industry for manufacturing transistors and integrated circuits. Doping silicon with trace amounts of Group 13 or Group 15 elements significantly alters its conductivity, forming p-type or n-type semiconductors.

Chemistry of Germanium, Tin, and Lead:

Germanium (Ge): A metalloid, primarily used as a semiconductor, though less common than silicon.
Tin (Sn): A metal, known for its two main allotropes: white tin (metallic) and gray tin (non-metallic, brittle). Used in solder, tin plating, and alloys like bronze. Its +2 and +4 oxidation states are both stable.
Lead (Pb): A soft, dense, malleable metal. Predominantly forms stable +2 compounds (e.g., PbO, PbCl₂) due to the inert pair effect, though +4 compounds exist (e.g., PbO₂). Historically used in plumbing and paints, but its toxicity has led to reduced usage.

This initial delve into the main group elements reveals a spectrum of fascinating chemical behaviors, from the explosive reactivity of alkali metals to the intricate structures of boranes and the unparalleled versatility of carbon and silicon. As we progress through subsequent chapters, we will continue to build upon this foundation, exploring the nuanced chemistries of the remaining main groups and the transition metals.

Chapter 6: Chemistry of Main Group Elements II (Groups 15, 16, 17, 18)

Our journey through the main group elements continues, delving into the fascinating and diverse chemistries of Groups 15, 16, 17, and 18. These groups encompass a wide array of elements, from the essential building blocks of life to the once-thought inert noble gases, each exhibiting unique properties and forming a myriad of compounds with significant applications in science and industry.

Group 15: The Nitrogen Group (Pnictogens)

Group 15, often called the pnictogens, consists of nitrogen (N), phosphorus (P), arsenic (As), antimony (Sb), and bismuth (Bi). This group showcases a remarkable transition from non-metallic character at the top to metallic character at the bottom. Nitrogen and phosphorus are non-metals, arsenic and antimony are metalloids, and bismuth is a metal.Diverse Oxidation States of Nitrogen and Phosphorus:

One of the most striking features of nitrogen and phosphorus is their ability to exhibit a wide range of oxidation states. Nitrogen, with its small size and high electronegativity, can exist in oxidation states from -3 to +5.

-3 Oxidation State: Ammonia (NH₃) is a classic example, where nitrogen has a -3 oxidation state. This compound is crucial in agriculture as a fertilizer and in industrial processes for synthesizing nitric acid and other nitrogenous compounds.
0 Oxidation State: Diatomic nitrogen (N₂) is the most abundant gas in our atmosphere. Its triple bond makes it incredibly stable and relatively unreactive under normal conditions.
+1 Oxidation State: Nitrous oxide (N₂O), commonly known as "laughing gas," finds use as an anesthetic and propellant.
+2 Oxidation State: Nitric oxide (NO) is a vital signaling molecule in biological systems, playing roles in vasodilation and neurotransmission.
+3 Oxidation State: Nitrous acid (HNO₂) and its salts (nitrites) are used as preservatives and in the synthesis of dyes.
+4 Oxidation State: Nitrogen dioxide (NO₂) is a reddish-brown gas involved in photochemical smog and is a precursor to acid rain.
+5 Oxidation State: Nitric acid (HNO₃), a strong oxidizing acid, is a cornerstone of the chemical industry, used in the production of fertilizers, explosives, and dyes.

Phosphorus, being larger and less electronegative than nitrogen, also exhibits diverse oxidation states, primarily -3, +3, and +5.

-3 Oxidation State: Phosphine (PH₃), analogous to ammonia, is a highly toxic gas used in fumigation.
+3 Oxidation State: Phosphorus trichloride (PCl₃) is a key reagent in organic synthesis, used to introduce phosphorus into molecules or to convert alcohols to alkyl chlorides.
+5 Oxidation State: Phosphorus pentachloride (PCl₅) is another important chlorinating agent, and phosphoric acid (H₃PO₄) and its salts are fundamental to biochemistry (e.g., ATP) and industrial applications (e.g., detergents, fertilizers).

Hydrides of Group 15:

The hydrides of Group 15 elements show a trend in stability and basicity. Ammonia (NH₃) is a stable gas, a weak base, and readily forms hydrogen bonds, leading to its relatively high boiling point. Phosphine (PH₃) is less stable and a weaker base than ammonia, and it does not exhibit significant hydrogen bonding. AsH₃, SbH₃, and BiH₃ become progressively less stable and more metallic in character.

Oxides of Group 15:

Nitrogen forms a remarkable series of oxides, as mentioned above, reflecting its varied oxidation states. Phosphorus also forms important oxides, notably phosphorus(III) oxide (P₄O₆) and phosphorus(V) oxide (P₄O₁₀). P₄O₁₀ is a potent dehydrating agent, used to remove water from gases and liquids.

Halides of Group 15:

Group 15 elements form various halides. Nitrogen forms relatively few stable halides, with NF₃ being the most common. Phosphorus, however, forms stable trihalides (PX₃, e.g., PCl₃) and pentahalides (PX₅, e.g., PCl₅), which are versatile reagents in organic and inorganic synthesis.

Here's a depiction of PCl₅.

Group 16: The Chalcogens

Group 16, known as the chalcogens (ore formers), comprises oxygen (O), sulfur (S), selenium (Se), tellurium (Te), and polonium (Po). Like Group 15, there's a trend from non-metallic oxygen and sulfur to the metallic polonium.

Oxygen and Sulfur Chemistry:

Oxygen is exceptionally reactive, forming compounds with almost all other elements. It is crucial for respiration, combustion, and various industrial processes.

Allotropes of Oxygen:

Dioxygen (O₂): The common form of oxygen, essential for life.
Ozone (O₃): A less stable allotrope with a distinctive pungent odor. Ozone in the stratosphere protects Earth from harmful UV radiation, while ground-level ozone is a pollutant.

Sulfur also exhibits a rich allotropy, far more extensive than oxygen. The most common and stable allotrope at room temperature is rhombic sulfur (S₈), which consists of crown-shaped rings. When heated, rhombic sulfur melts into a mobile yellow liquid, which darkens and becomes highly viscous as the rings open and polymerize. Rapid cooling of this viscous liquid yields plastic sulfur, an amorphous form.Important Compounds of Oxygen and Sulfur:

Water (H₂O): The most vital compound of oxygen, essential for all known life forms. Its unique properties are due to extensive hydrogen bonding.
Hydrogen Peroxide (H₂O₂): A strong oxidizing agent used as a disinfectant and bleach.
Sulfur Dioxide (SO₂): A pungent gas produced during the combustion of fossil fuels, contributing to acid rain. It is also an important intermediate in the production of sulfuric acid.
Sulfur Trioxide (SO₃): The anhydride of sulfuric acid, highly reactive and involved in the contact process for sulfuric acid production.
Hydrogen Sulfide (H₂S): A highly toxic gas with a characteristic rotten egg smell, often found in natural gas and volcanic emissions.
Sulfuric Acid (H₂SO₄): The world's most widely produced industrial chemical, used in fertilizers, batteries, and chemical synthesis. Here's an illustration of Sulfuric Acid's chemical formula:

Group 17: The Halogens

Group 17, the halogens (salt-formers), consists of fluorine (F), chlorine (Cl), bromine (Br), iodine (I), and astatine (At). These highly reactive non-metals are characterized by their strong oxidizing power and their tendency to gain an electron to form a -1 oxidation state.

Reactivity of Halogens:

The reactivity of halogens decreases down the group from fluorine to iodine. Fluorine is the most reactive element, capable of reacting with almost all other elements, including noble gases under certain conditions. This extreme reactivity is due to its high electronegativity and the low dissociation energy of the F-F bond.

Fluorine: Used in the production of Teflon (polytetrafluoroethylene), refrigerants, and in enriching uranium (as UF₆).
Chlorine: A powerful disinfectant for water treatment, also used in the production of PVC, bleaches, and numerous organic chemicals.
Bromine: Used in flame retardants, pharmaceuticals, and photographic chemicals.
Iodine: Essential for thyroid hormone production, also used as an antiseptic and in analytical chemistry.

Properties of Interhalogen Compounds:

Interhalogen compounds are formed between two different halogens. Their general formula is XYn, where X is the larger (less electronegative) halogen and Y is the smaller (more electronegative) halogen, and n can be 1, 3, 5, or 7.

XY type: Chlorine monofluoride (ClF), Bromine monofluoride (BrF), Iodine monochloride (ICl). ICl is a solid at room temperature and resembles elemental bromine in color and physical properties.
XY₃ type: Chlorine trifluoride (ClF₃), Bromine trifluoride (BrF₃), Iodine trichloride (ICl₃). ClF₃ is a very powerful fluorinating agent, capable of igniting many substances on contact.
XY₅ type: Bromine pentafluoride (BrF₅), Iodine pentafluoride (IF₅).
XY₇ type: Iodine heptafluoride (IF₇).

These compounds are generally more reactive than the parent halogens (except F₂), with their reactivity increasing with the difference in electronegativity between the two halogens. They are powerful oxidizing and fluorinating/chlorinating agents.

Group 18: The Noble Gases

Group 18 consists of helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), and radon (Rn). Historically, these elements were considered "inert" due to their full valence electron shells, leading to extreme stability and low reactivity. However, over the past few decades, a rich chemistry of noble gas compounds has emerged, particularly for the heavier elements.

Increasingly Rich Chemistry of Noble Gas Compounds:

The heavier noble gases, particularly xenon, have sufficiently large atomic radii and lower ionization energies to allow for bond formation, especially with highly electronegative elements like fluorine and oxygen.

Xenon Fluorides:
- Xenon difluoride (XeF₂): The simplest stable xenon fluoride, a white crystalline solid. It is a mild fluorinating agent and has a linear molecular geometry.

Chapter 7: Introduction to Transition Metal Chemistry and Ligand Field TheoryTransition metals, often referred to as the d-block elements, occupy a unique and central position in the periodic table, spanning groups 3 through 12. Their distinctive properties set them apart from main group elements and make them indispensable in numerous chemical, biological, and industrial processes.

This chapter will delve into the fascinating world of transition metals, exploring their characteristic features such as variable oxidation states, the formation of vibrantly colored compounds, and their unparalleled catalytic activity. We will begin by examining their electron configurations and common oxidation states, laying the groundwork for a deeper understanding of their reactivity. The central pillar of this chapter will be Ligand Field Theory (LFT), a sophisticated model that extends the principles of crystal field theory to provide a comprehensive explanation for the bonding, magnetic properties, and electronic spectra of transition metal complexes. Concepts such as crystal field splitting, the distinction between high-spin and low-spin complexes, and the intriguing phenomenon of Jahn-Teller distortion will be meticulously covered.

Electron Configurations and Common Oxidation States The defining characteristic of transition metals is the presence of incompletely filled d orbitals in at least one of their common oxidation states. For instance, consider the first-row transition metals (Scandium to Zinc). Their general electron configuration is [Noble Gas] (n-1)d

 x^xx

 y^yy

. However, there's a nuance: while electrons typically fill the 4s orbital before the 3d orbital in the atomic state, upon ionization, the 4s electrons are typically removed first. This leads to a rich array of possible oxidation states, contributing significantly to their diverse chemistry.Let's take Iron (Fe) as a prime example. Its atomic electron configuration is [Ar] 3d

 6^66

 2^22

. Common oxidation states for iron include +2 and +3.

Fe
```
 2+^{2+}2+ 
```
: [Ar] 3d
```
 6^66 
```
(loses the two 4s electrons)
Fe
```
 3+^{3+}3+ 
```
: [Ar] 3d
```
 5^55 
```
(loses the two 4s electrons and one 3d electron)

This ability to readily switch between oxidation states makes transition metals excellent catalysts and crucial components in redox reactions. For instance, the conversion of Fe

 2+^{2+}2+

to Fe

 3+^{3+}3+

and vice-versa is vital in biological processes like oxygen transport by hemoglobin.Another example is Copper (Cu). Its atomic configuration is [Ar] 3d

 10^{10}10

 1^11

(an exception to the general filling rule due to the stability of a full d-subshell). Common oxidation states are +1 and +2.

Cu
```
 +^++ 
```
: [Ar] 3d
```
 10^{10}10 
```
(loses the 4s electron)
Cu
```
 2+^{2+}2+ 
```
: [Ar] 3d
```
 9^99 
```
(loses the 4s electron and one 3d electron)
The Cu
```
 2+^{2+}2+ 
```
ion, with its unpaired electron, is responsible for the characteristic blue color of many copper compounds.

Variable Oxidation States: A Practical ExampleThe industrial production of ammonia via the Haber-Bosch process relies on a transition metal catalyst, typically iron. The iron catalyst cycles through various oxidation states, facilitating the reaction between nitrogen and hydrogen gases. While the precise mechanism is complex, the ability of iron to accommodate different electron counts in its d-orbitals is key to its catalytic activity, acting as an electron reservoir and transfer agent.Colorful Compounds: A Visual DelightOne of the most striking features of transition metals is the vibrant colors of their compounds, both in solid state and in solution. Unlike main group metal ions, which are typically colorless (e.g., Na

 +^++

, Mg

 2+^{2+}2+

), transition metal complexes exhibit a spectrum of hues. This phenomenon is directly linked to their partially filled d orbitals and is elegantly explained by Ligand Field Theory.

For instance, a solution of nickel(II) salts is typically green (e.g., [Ni(H

 2_22

 6_66

]

 2+^{2+}2+

). Cobalt(II) salts are often pink or blue depending on the ligands (e.g., [Co(H

 2_22

 6_66

]

 2+^{2+}2+

is pink, while [CoCl

 4_44

]

 2−^{2-}2−

is blue). Chromium(III) compounds can be violet, green, or red (e.g., [Cr(H

 2_22

 6_66

]

 3+^{3+}3+

is violet).

These colors arise from electronic transitions between the split d orbitals, as we will explore with LFT.Catalytic Activity: Driving Chemical ProgressTransition metals are unparalleled as catalysts, accelerating reaction rates without being consumed in the process. Their variable oxidation states and ability to form stable intermediates with reactants are fundamental to their catalytic prowess.Example: Hydrogenation Reactions

Many industrial processes involve hydrogenation, where hydrogen is added across a double or triple bond. Palladium (Pd) and Platinum (Pt) catalysts are widely used for this purpose. For example, the hydrogenation of vegetable oils to produce margarine uses nickel or palladium catalysts. The metal surface provides sites where hydrogen molecules can dissociate and bind to the unsaturated organic substrate, facilitating the addition.

Example: Ziegler-Natta Catalysis

The polymerization of alkenes to produce plastics like polyethylene and polypropylene heavily relies on Ziegler-Natta catalysts, which are often based on titanium (Ti) and aluminum (Al) compounds. These catalysts provide a coordination site for the alkene monomer, allowing for its insertion and growth of the polymer chain.

Ligand Field Theory (LFT) Ligand Field Theory is a quantum mechanical model that describes the bonding in transition metal complexes, extending the purely electrostatic assumptions of Crystal Field Theory (CFT) by incorporating covalent character into the metal-ligand interactions. It successfully explains the magnetic properties, colors, and stability of these complexes.

Crystal Field Splitting In an isolated transition metal ion, the five d orbitals (d

 xy_{xy}xy

, d

 xz_{xz}xz

, d

 yz_{yz}yz

, d

 x2−y2_{x^2-y^2}x2−y2

, and d

 z2_{z^2}z2

) are degenerate, meaning they have the same energy. However, when ligands (molecules or ions that donate electron pairs to the metal) approach the central metal ion, their lone pair electrons create an electrostatic field that interacts with the d orbitals. This interaction lifts the degeneracy, splitting the d orbitals into different energy levels. This phenomenon is called crystal field splitting.Let's consider an octahedral complex, the most common geometry. In an octahedral environment, six ligands approach the metal ion along the x, y, and z axes. The d

 x2−y2_{x^2-y^2}x2−y2

and d

 z2_{z^2}z2

orbitals have lobes pointing directly along these axes, experiencing greater repulsion from the ligand lone pairs. Consequently, their energy increases. These two orbitals form the e

 g_gg

set (doubly degenerate). The d

 xy_{xy}xy

, d

 xz_{xz}xz

, and d

 yz_{yz}yz

orbitals have lobes that point between the axes, experiencing less repulsion. Their energy decreases. These three orbitals form the t

 2g_{2g}2g

set (triply degenerate).The energy difference between the e

 g_gg

and t

 2g_{2g}2g

sets is called the crystal field splitting energy (Δ

 o_oo

or 10 Dq). This energy gap is crucial in determining the complex's properties.

Chapter 8: Coordination Chemistry:

Structure, Isomerism, and ReactivityCoordination chemistry is a fascinating and diverse field that explores compounds formed between a central metal atom or ion and a surrounding array of molecules or ions called ligands. Building upon the foundational understanding of Ligand Field Theory (LFT), this chapter delves deeper into the intricate world of coordination complexes, examining their diverse geometries, the various forms of isomerism they exhibit, and the fundamental principles governing their reactivity.

Geometries of Coordination Complexes

The geometry of a coordination complex is determined primarily by the coordination number of the central metal ion (the number of ligands directly bonded to it) and the electronic configuration of the metal. Common geometries include:

Linear (Coordination Number 2):While less common for transition metals, some complexes with two ligands can adopt a linear geometry.
- Practical Example:The diamminesilver(I) ion,
```
 [Ag(NH3)2]+[Ag(NH_3)_2]^+[Ag(NH3)2]+ 
```
  , is a classic example of a linear complex. The two ammonia ligands are positioned 180 degrees apart around the central silver ion. This geometry is favored for
```
 d10d^{10}d10 
```
  metal ions.
Tetrahedral (Coordination Number 4):In a tetrahedral complex, the central metal ion is surrounded by four ligands positioned at the vertices of a tetrahedron. The bond angles are typically 109.5 degrees. This geometry is often observed for complexes of
```
 d0d^{0}d0 
```
and
```
 d10d^{10}d10 
```
metal ions, and also for
```
 d5d^{5}d5 
```
,
```
 d6d^{6}d6 
```
,
```
 d7d^{7}d7 
```
, and
```
 d8d^{8}d8 
```
ions with weak-field ligands.
- Practical Example:The tetrachloronickelate(II) ion,
```
 [NiCl4]2−[NiCl_4]^{2-}[NiCl4]2− 
```
  , often adopts a tetrahedral geometry, especially when formed with weak-field chloride ligands. The four chloride ions are arranged tetrahedrally around the nickel(II) ion.
Square Planar (Coordination Number 4):This geometry is characteristic of many
```
 d8d^8d8 
```
metal ions, particularly those from the second and third transition series (e.g., Pt(II), Pd(II), Au(III)). The four ligands and the central metal ion lie in the same plane, with bond angles of 90 degrees.
- Practical Example:Cisplatin,
```
 cisciscis 
```
  -
```
 [PtCl2(NH3)2][PtCl_2(NH_3)_2][PtCl2(NH3)2] 
```
  , a widely used anticancer drug, is a quintessential square planar complex. The platinum(II) ion is at the center, surrounded by two chloride ions and two ammonia molecules in a square planar arrangement.

Trigonal Bipyramidal (Coordination Number 5):In this geometry, three ligands lie in an equatorial plane, and two ligands are axial, perpendicular to the equatorial plane.
- Practical Example:Iron pentacarbonyl,
```
 [Fe(CO)5][Fe(CO)_5][Fe(CO)5] 
```
  , exhibits a trigonal bipyramidal structure. Three carbonyl ligands are in the equatorial plane, and two are in the axial positions.
Octahedral (Coordination Number 6):This is the most common geometry for transition metal complexes. The central metal ion is surrounded by six ligands positioned at the vertices of an octahedron, resulting in 90-degree bond angles between adjacent ligands.
- Practical Example:The hexaaquachromium(III) ion,
```
 [Cr(H2O)6]3+[Cr(H_2O)_6]^{3+}[Cr(H2O)6]3+ 
```
  , is an excellent example of an octahedral complex. Six water molecules are coordinated to the central chromium(III) ion.

Isomerism in Coordination Compounds

Isomers are compounds that have the same chemical formula but different arrangements of atoms. In coordination chemistry, isomerism is particularly rich and diverse, leading to a vast array of compounds with distinct properties.

Structural Isomerism:These isomers differ in the connectivity of the atoms.
- Linkage Isomerism:Occurs when an ambidentate ligand (a ligand that can bind to the metal through more than one donor atom) binds through different atoms.
  - Practical Example:The nitrite ion (
```
 NO2−NO_2^-NO2− 
```
    ) can bind through nitrogen (nitro,
```
 −NO2-NO_2−NO2 
```
    ) or oxygen (nitrito,
```
 −ONO-ONO−ONO 
```
    ). Consider the complex
```
 [Co(NH3)5(NO2)]Cl2[Co(NH_3)_5(NO_2)]Cl_2[Co(NH3)5(NO2)]Cl2 
```
    . One isomer has the
```
 NO2−NO_2^-NO2− 
```
    ligand bonded via nitrogen (pentaamminenitrocobalt(III) chloride), while the linkage isomer has it bonded via oxygen (pentaamminenitritocobalt(III) chloride). These two isomers have different colors and spectroscopic properties.
- Hydration (Solvate) Isomerism:Occurs when water molecules are exchanged between the coordination sphere and the crystal lattice.
  - Practical Example:Consider chromium(III) chloride hexahydrate,
```
 CrCl3⋅6H2OCrCl_3 \cdot 6H_2OCrCl3⋅6H2O 
```
    . It exists as several hydration isomers:
    - ```
     [Cr(H2O)6]Cl3[Cr(H_2O)_6]Cl_3[Cr(H2O)6]Cl3 
```
  (violet) - all six water molecules are coordinated.
- ```
 [Cr(H2O)5Cl]Cl2⋅H2O[Cr(H_2O)_5Cl]Cl_2 \cdot H_2O[Cr(H2O)5Cl]Cl2⋅H2O 
```
      (light green) - five water molecules and one chloride are coordinated, with one water molecule as crystal water.
    - ```
     [Cr(H2O)4Cl2]Cl⋅2H2O[Cr(H_2O)_4Cl_2]Cl \cdot 2H_2O[Cr(H2O)4Cl2]Cl⋅2H2O 
```
  (dark green) - four water molecules and two chlorides are coordinated, with two water molecules as crystal water.
- Ionization Isomerism:Arises when the counter ion in a complex salt is itself a potential ligand and can displace a ligand that is coordinated to the metal ion to become part of the coordination sphere.
  - Practical Example:Consider the compounds with the formula
```
 CoCl3⋅5NH3⋅SO4CoCl_3 \cdot 5NH_3 \cdot SO_4CoCl3⋅5NH3⋅SO4 
```
    .
    - ```
     [Co(NH3)5SO4]Cl[Co(NH_3)_5SO_4]Cl[Co(NH3)5SO4]Cl 
```
  (pentaamminesulfatocobalt(III) chloride) - the sulfate ion is coordinated, and chloride is the counter ion.
- ```
 [Co(NH3)5Cl]SO4[Co(NH_3)_5Cl]SO_4[Co(NH3)5Cl]SO4 
```
      (pentaamminechlorocobalt(III) sulfate) - the chloride ion is coordinated, and sulfate is the counter ion. These isomers react differently with
```
 AgNO3AgNO_3AgNO3 
```
      (to precipitate
```
 AgClAgClAgCl 
```
      ) and
```
 BaCl2BaCl_2BaCl2 
```
      (to precipitate
```
 BaSO4BaSO_4BaSO4 
```
      ).
- Coordination Isomerism:Occurs in salts where both the cation and anion are complex ions, and the ligands are distributed differently between the two metal centers.
  - Practical Example:In
```
 [Co(NH3)6][Cr(CN)6][Co(NH_3)_6][Cr(CN)_6][Co(NH3)6][Cr(CN)6] 
```
    (hexamminecobalt(III) hexacyanochromate(III)), the ammonia ligands are with cobalt and cyanide with chromium. Its coordination isomer is
```
 [Cr(NH3)6][Co(CN)6][Cr(NH_3)_6][Co(CN)_6][Cr(NH3)6][Co(CN)6] 
```
    (hexamminechromium(III) hexacyanocobaltate(III)), where the ligands are swapped.
Stereoisomerism:These isomers have the same connectivity but differ in the spatial arrangement of atoms.
- Geometric (Cis-Trans) Isomerism:Found in square planar and octahedral complexes when there are different ligands.
  - Square Planar (e.g.,
```
 MA2B2MA_2B_2MA2B2 
```
    type):
    - Practical Example:Cisplatin,
```
 cisciscis 
```
      -
```
 [PtCl2(NH3)2][PtCl_2(NH_3)_2][PtCl2(NH3)2] 
```
      , has the two ammonia ligands adjacent to each other (90 degrees apart), and the two chloride ligands adjacent. Its trans isomer,
      transtranstrans
      -
```
 [PtCl2(NH3)2][PtCl_2(NH_3)_2][PtCl2(NH3)2] 
```
      , has the two ammonia ligands opposite each other (180 degrees apart), as do the chloride ligands. These isomers have profoundly different biological activities.

Octahedral (e.g.,
```
 MA4B2MA_4B_2MA4B2 
```
type):
* Practical Example:The complex
```
 [Co(NH3)4Cl2]+[Co(NH_3)_4Cl_2]^+[Co(NH3)4Cl2]+ 
```
exists as cis and trans isomers. In the cis isomer, the two chloride ligands are adjacent, forming a 90-degree angle. In the trans isomer, the two chloride ligands are opposite, forming a 180-degree angle. They have different colors (the cis is purple, the trans is green).
* Octahedral (e.g.,
MA3B3MA_3B_3MA3B3
type - Fac/Mer Isomerism):
* Practical Example:In complexes like
```
 [Co(NH3)3Cl3][Co(NH_3)_3Cl_3][Co(NH3)3Cl3] 
```
, the three identical ligands (e.g.,
```
 NH3NH_3NH3 
```
) can be on one face of the octahedron (facial or fac isomer) or arranged around an equator (meridional or merisomer).
- Optical (Enantiomeric) Isomerism:Occurs when a complex and its mirror image are non-superimposable (chiral). These isomers rotate plane-polarized light in opposite directions.
  - Practical Example:Octahedral complexes with bidentate ligands often exhibit optical isomerism. For instance, the complex
```
 [Co(en)3]3+[Co(en)_3]^{3+}[Co(en)3]3+ 
```
    (where 'en' is ethylenediamine, a bidentate ligand) is chiral. It exists as two enantiomers, denoted as
```
 Δ\DeltaΔ 
```
    and
```
 Λ\LambdaΛ 
```
    , which are non-superimposable mirror images of each other. These enantiomers rotate plane-polarized light in opposite directions.

Reactivity of Coordination Complexes

The reactivity of coordination complexes is central to their applications in catalysis, medicine, and materials science. Two major types of reactions are prevalent: ligand substitution and electron transfer.

Ligand Substitution Reactions:These reactions involve the exchange of one or more ligands in the coordination sphere of a metal ion for other ligands. The mechanisms can vary significantly depending on the metal, its oxidation state, and the nature of the ligands.
- Associative (A) Mechanism:Involves the formation of an intermediate with an increased coordination number. The incoming ligand first binds to the metal, then the leaving ligand departs. This is common for square planar complexes.
  - Practical Example:The substitution of chloride in
```
 transtranstrans 
```
    -
```
 [PtCl2(NH3)2][PtCl_2(NH_3)_2][PtCl2(NH3)2] 
```
    by pyridine (
```
 pypypy 
```
    ) often proceeds via an associative mechanism. The pyridine first associates with the Pt(II) center, forming a five-coordinate intermediate, before a chloride ion departs.
  - ```
   Pt(NH3)2Cl2+py→[Pt(NH3)2Cl2(py)]→[Pt(NH3)2Cl(py)]Cl+Cl−Pt(NH_3)_2Cl_2 + py \rightarrow [Pt(NH_3)_2Cl_2(py)] \rightarrow [Pt(NH_3)_2Cl(py)]Cl + Cl^-Pt(NH3)2Cl2+py→[Pt(NH3)2Cl2(py)]→[Pt(NH3)2Cl(py)]Cl+Cl− 
```
- Dissociative (D) Mechanism:Involves the departure of a ligand to form an intermediate with a decreased coordination number, followed by the binding of the incoming ligand. This is common for octahedral complexes.
  - Practical Example:The hydrolysis of
```
 [Co(NH3)5Cl]2+[Co(NH_3)_5Cl]^{2+}[Co(NH3)5Cl]2+ 
```
    to
```
 [Co(NH3)5(H2O)]3+[Co(NH_3)_5(H_2O)]^{3+}[Co(NH3)5(H2O)]3+ 
```
    typically proceeds via a dissociative mechanism. The chloride ligand first departs, forming a five-coordinate intermediate
```
 [Co(NH3)5]3+[Co(NH_3)_5]^{3+}[Co(NH3)5]3+ 
```
    , which then rapidly reacts with water.
  - ```
   [Co(NH3)5Cl]2+→[Co(NH3)5]3++Cl−→[Co(NH3)5(H2O)]3+[Co(NH_3)_5Cl]^{2+} \rightarrow [Co(NH_3)_5]^{3+} + Cl^- \rightarrow [Co(NH_3)_5(H_2O)]^{3+}[Co(NH3)5Cl]2+→[Co(NH3)5]3++Cl−→[Co(NH3)5(H2O)]3+ 
```
- Interchange (I) Mechanism:Both association and dissociation occur in a concerted step, without a distinct intermediate. Further categorized as associative interchange (
```
 IaI_aIa 
```
  ) or dissociative interchange (
```
 IdI_dId 
```
  ) depending on the relative importance of bond making and bond breaking.
  - Practical Example:Many octahedral complexes, particularly those of first-row transition metals, undergo ligand substitution via interchange mechanisms. For instance, the exchange of water ligands in hexaaqua metal ions (
```
 [M(H2O)6]n+[M(H_2O)_6]^{n+}[M(H2O)6]n+ 
```
    ) with other ligands often follows an
```
 IdI_dId 
```
    mechanism, where water slowly dissociates while the incoming ligand starts to bind.
Electron Transfer Reactions (Redox Reactions):These reactions involve the transfer of electrons between metal centers in coordination complexes, leading to changes in their oxidation states. They are fundamental in biological processes and catalysis.
- Outer-Sphere Electron Transfer:Electron transfer occurs without direct bond formation between the two reacting metal centers. The electron 'tunnels' through the intact coordination spheres of the reactants. This typically occurs when ligands are inert or when a direct approach is sterically hindered.
  - Practical Example:The reduction of
```
 [Fe(phen)3]3+[Fe(phen)_3]^{3+}[Fe(phen)3]3+ 
```
    by
```
 [Ru(bpy)3]2+[Ru(bpy)_3]^{2+}[Ru(bpy)3]2+ 
```
    (where phen = 1,10-phenanthroline and bpy = 2,2'-bipyridine, both inert ligands) is a classic outer-sphere reaction. The electron transfers directly from the ruthenium complex to the iron complex without any ligand exchange or bridging.
  - ```
   [Ru(bpy)3]2++[Fe(phen)3]3+→[Ru(bpy)3]3++[Fe(phen)3]2+[Ru(bpy)_3]^{2+} + [Fe(phen)_3]^{3+} \rightarrow [Ru(bpy)_3]^{3+} + [Fe(phen)_3]^{2+}[Ru(bpy)3]2++[Fe(phen)3]3+→[Ru(bpy)3]3++[Fe(phen)3]2+ 
```
- Inner-Sphere Electron Transfer:Electron transfer occurs through a bridging ligand that is common to both metal centers. One of the ligands from one complex forms a bond with the other metal center, creating a 'bridge' for electron transfer. After the electron transfer, the bridge usually breaks. This mechanism is favored when at least one of the reactants is labile.
  - Practical Example:The reduction of
```
 [Co(NH3)5Cl]2+[Co(NH_3)_5Cl]^{2+}[Co(NH3)5Cl]2+ 
```
    by
```
 [Cr(H2O)6]2+[Cr(H_2O)_6]^{2+}[Cr(H2O)6]2+ 
```
    proceeds via an inner-sphere mechanism. The chloride ligand from the cobalt complex bridges to the chromium(II) ion, forming an intermediate
```
 [(NH3)5Co−Cl−Cr(H2O)5]4+[(NH_3)_5Co-Cl-Cr(H_2O)_5]^{4+}[(NH3)5Co−Cl−Cr(H2O)5]4+ 
```
    . The electron transfers across the chloride bridge, reducing Co(III) to Co(II) and oxidizing Cr(II) to Cr(III). The bridge then breaks, leading to
```
 [Co(H2O)6]2+[Co(H_2O)_6]^{2+}[Co(H2O)6]2+ 
```
    (or other labile Co(II) products) and
```
 [Cr(H2O)5Cl]2+[Cr(H_2O)_5Cl]^{2+}[Cr(H2O)5Cl]2+ 
```
    .
  - ```
   [Co(NH3)5Cl]2++[Cr(H2O)6]2+→[(NH3)5Co−Cl−Cr(H2O)5]4+→[Co(H2O)6]2++[Cr(H2O)5Cl]2+[Co(NH_3)_5Cl]^{2+} + [Cr(H_2O)_6]^{2+} \rightarrow [(NH_3)_5Co-Cl-Cr(H_2O)_5]^{4+} \rightarrow [Co(H_2O)_6]^{2+} + [Cr(H_2O)_5Cl]^{2+}[Co(NH3)5Cl]2++[Cr(H2O)6]2+→[(NH3)5Co−Cl−Cr(H2O)5]4+→[Co(H2O)6]2++[Cr(H2O)5Cl]2+ 
```

In conclusion, coordination chemistry is a vast and dynamic field. Understanding the various geometries, the multitude of isomeric forms, and the mechanisms of ligand substitution and electron transfer reactions is crucial for comprehending the behavior and applications of these important compounds in various scientific and technological domains. The precise control over these structural and reactive properties allows for the design of sophisticated catalysts, novel pharmaceuticals, and advanced materials.

Chapter 9: Organometallic Chemistry: Fundamentals and Applications

Organometallic chemistry represents a captivating frontier at the intersection of inorganic and organic chemistry. It is the study of compounds containing a direct, stoichiometric, and at least somewhat stable bond between a metal and a carbon atom. This unique bonding arrangement bestows upon organometallic compounds extraordinary reactivity and selectivity, making them indispensable in academic research, industrial catalysis, and the synthesis of pharmaceuticals and advanced materials. From the simplest Grignard reagents to complex catalytic cycles, organometallic chemistry underpins a vast array of modern chemical transformations.

The Nature of the Metal-Carbon Bond

The defining characteristic of organometallic chemistry is the metal-carbon (M-C) bond. This bond can vary significantly in character, ranging from highly ionic to predominantly covalent, depending on the electronegativity difference between the metal and the carbon atom.

Ionic M-C bonds:Typically found with highly electropositive metals from Groups 1 and 2 (alkali and alkaline earth metals). For instance, methyl lithium (CH₃Li) exhibits a highly polar M-C bond, where the carbon atom carries significant negative charge, making it a powerful nucleophile and base. This ionic character is a major reason why organolithium and organomagnesium (Grignard) reagents are so reactive and useful in organic synthesis.
- Practical Example: The reaction of methyl lithium with benzaldehyde to form 1-phenylethanol. The highly nucleophilic methyl carbanion attacks the electrophilic carbonyl carbon.
  CH₃Li + C₆H₅CHO → C₆H₅CH(OLi)CH₃ → (after workup) C₆H₅CH(OH)CH₃

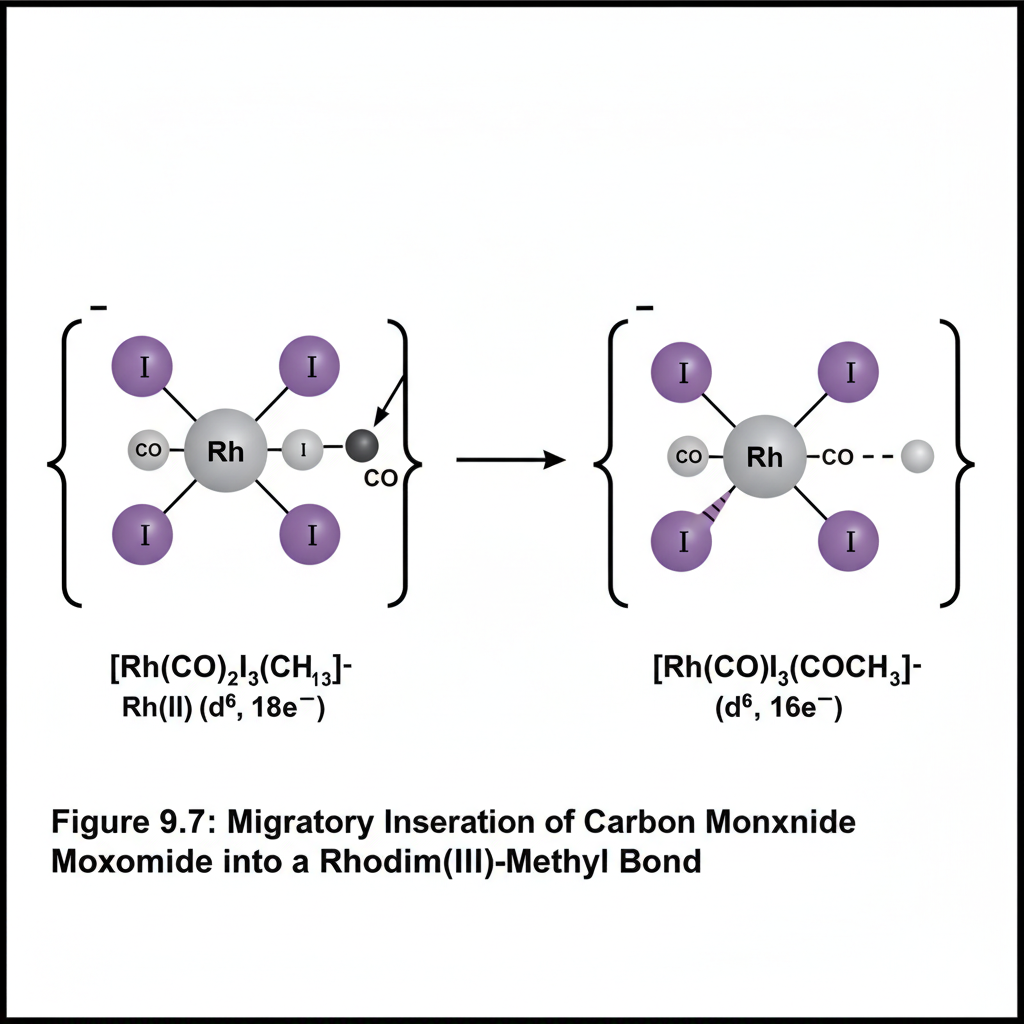
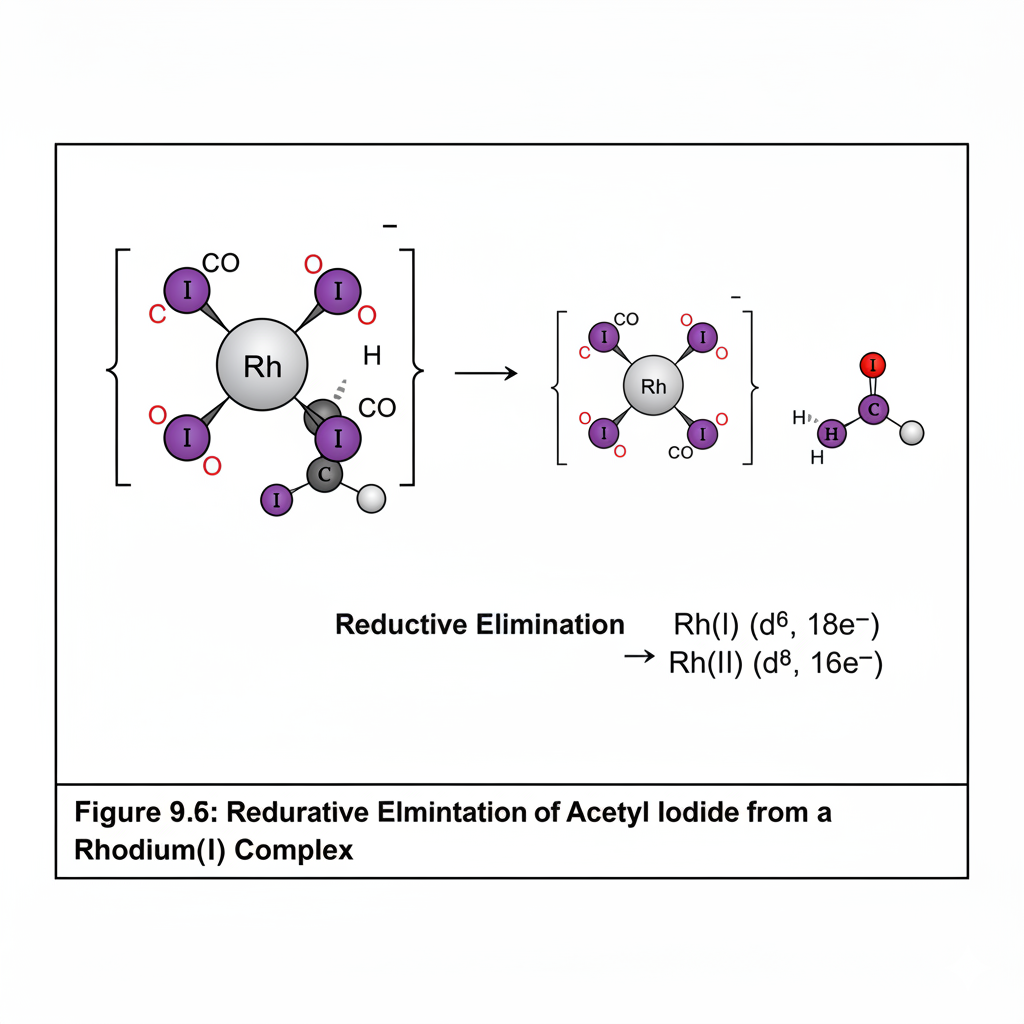
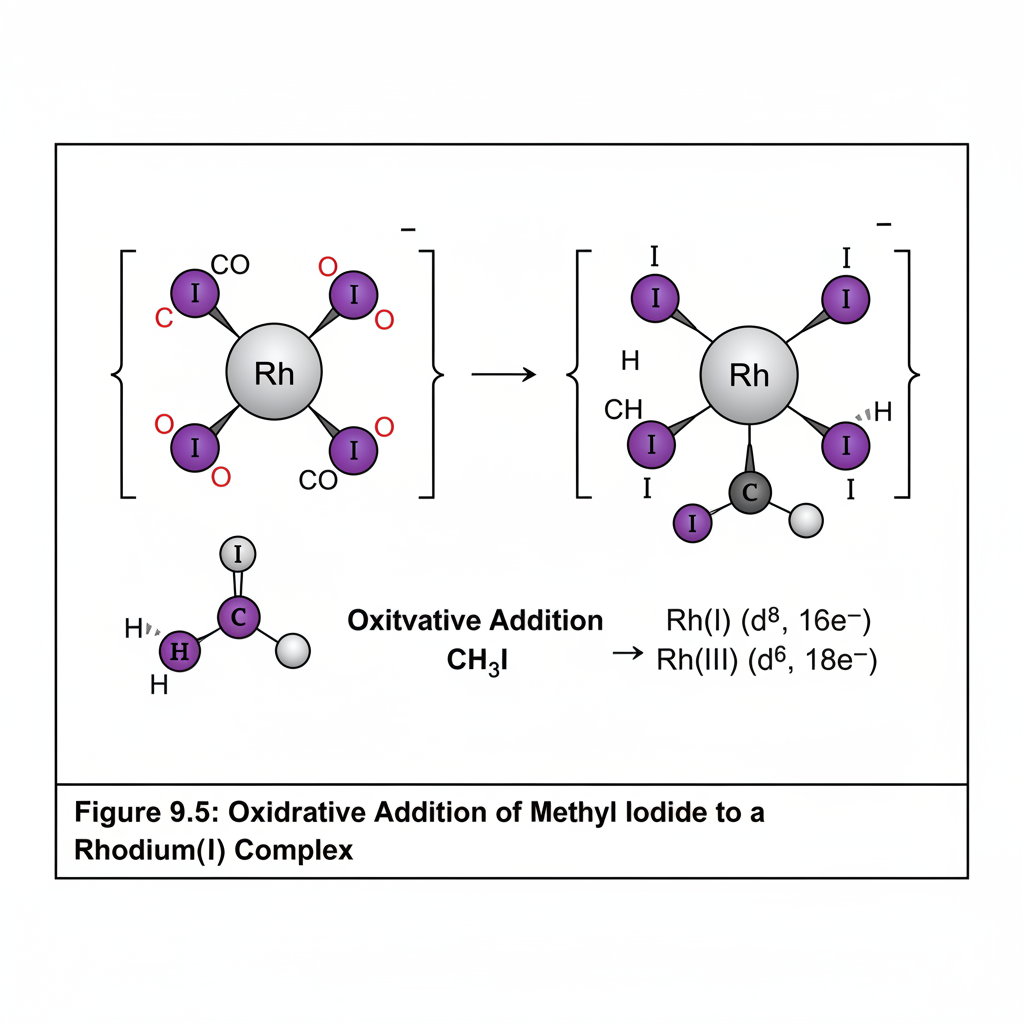
Covalent M-C bonds:Prevalent with transition metals and heavier main group metals. These bonds often have significant covalent character, involving orbital overlap between the metal and carbon. The nature of this overlap can range from sigma (σ) bonds, as in metal alkyls, to more complex π-type interactions in metal-alkene or metal-cyclopentadienyl complexes. The strength and reactivity of these covalent bonds are fine-tuned by the electronic properties of the metal and the other ligands present.
- Practical Example: Dimethylmercury ((CH₃)₂Hg), a highly toxic but historically important organometallic compound. The Hg-C bond here is largely covalent.

Common Organometallic Ligands

Ligands are atoms or molecules that bind to a central metal atom. In organometallic chemistry, these ligands contain carbon atoms directly bonded to the metal center. Their ability to donate electrons to the metal significantly influences the metal's electronic state, reactivity, and stability.

Carbonyls (CO):Perhaps the most iconic organometallic ligand. Carbon monoxide is a strong σ-donor (from the carbon lone pair) and a powerful π-acceptor (back-bonding from filled metal d-orbitals into empty CO π* orbitals). This synergistic bonding strengthens the M-CO bond.
- Practical Example: Nickel tetracarbonyl (Ni(CO)₄), a volatile and highly toxic compound used in the Mond process for purifying nickel.

Alkyls (R):Organic groups (e.g., methyl, ethyl, phenyl) bonded to the metal via a single carbon atom. They typically act as 1-electron (neutral ligand method) or 2-electron (ionic ligand method) σ-donors.
- Practical Example: Trimethylaluminum (Al(CH₃)₃), a pyrophoric liquid used in Ziegler-Natta catalysis for olefin polymerization.
Alkenes and Alkynes:Unsaturated hydrocarbons that bind to metals via their π-electron systems. They donate electron density from their filled π-orbitals to empty metal d-orbitals and accept electron density from filled metal d-orbitals into their empty π*-orbitals (π-backbonding). They are typically 2-electron donors.
- Practical Example: Zeise's salt (K[PtCl₃(C₂H₄)]), one of the first recognized organometallic compounds, where ethylene is bound side-on to platinum.
Cyclopentadienyls (Cp, C₅H₅⁻):A highly stable and ubiquitous ligand in organometallic chemistry. It binds to metals in an η⁵ (pentahapto) fashion, meaning all five carbon atoms are simultaneously coordinated to the metal. It's a 6-electron donor.
- Practical Example: Ferrocene ((η⁵-C₅H₅)₂Fe), a remarkably stable "sandwich" compound, often considered the archetypal organometallic compound.

The 18-Electron Rule

The 18-electron rule is a useful guideline for predicting the stability and reactivity of transition metal organometallic complexes. It states that stable complexes often achieve an 18-electron valence shell, analogous to the octet rule for main group elements. This corresponds to filling the s, p, and d orbitals in the metal's valence shell (1 s orbital + 3 p orbitals + 5 d orbitals = 9 orbitals, each accommodating 2 electrons, totaling 18 electrons).To apply the rule, we sum the metal's d-electron count and the electron contributions from all ligands. There are two common methods:

Neutral Ligand (Covalent) Method:
- Metal d-electron count: Equal to the group number (for d-block elements).
- Ligand contributions: Each ligand contributes its electrons as if it were a neutral species (e.g., CO = 2e⁻, C₂H₄ = 2e⁻, alkyl (R) = 1e⁻, Cp = 5e⁻).
- Add any charge to the total.
Ionic Ligand (Oxidation State) Method:
- Metal d-electron count: Group number - oxidation state.
- Ligand contributions: Each ligand contributes its electrons as if it were an anion (e.g., CO = 2e⁻, C₂H₄ = 2e⁻, alkyl (R⁻) = 2e⁻, Cp⁻ = 6e⁻).
- The overall charge is then the sum of the charges of the metal and ligands.

Practical Example: Let's apply the 18-electron rule to Cr(CO)₆ (Chromium hexacarbonyl).

Neutral Ligand Method:
- Chromium (Group 6) = 6 valence electrons
- 6 CO ligands x 2 electrons/CO = 12 electrons
- Total = 6 + 12 = 18 electrons. This predicts stability, which is observed for Cr(CO)₆.
Ionic Ligand Method:
- Assume CO is neutral. So Cr is in the 0 oxidation state.
- Chromium (0) has 6 d-electrons.
- 6 CO ligands x 2 electrons/CO = 12 electrons
- Total = 6 + 12 = 18 electrons.

While a useful guideline, the 18-electron rule is not universally obeyed, especially for early or late transition metals, or square planar d⁸ complexes (which often prefer 16 electrons).

Key Reactions in Organometallic Chemistry

Organometallic reactions are characterized by changes in the oxidation state and coordination number of the metal center, as well as the nature of the metal-ligand bonds. Understanding these fundamental steps is crucial for designing catalytic cycles.

Oxidative Addition (OA):A process where a molecule (e.g., H₂, R-X, O₂) adds to a metal center, increasing the metal's oxidation state by +2 and its coordination number by +2. Both fragments of the added molecule become new ligands. This requires the metal to have two vacant coordination sites and be in a relatively low oxidation state.
- General form: Mⁿ + A-B → A-Mⁿ⁺²-B
- Practical Example: The addition of methyl iodide (CH₃I) to a rhodium(I) complex in the Monsanto acetic acid process.
  [Rh(CO)₂I₂]⁻ + CH₃I → [Rh(CO)₂I₃(CH₃)]⁻
  Here, Rh(I) (d⁸, 16e⁻) undergoes oxidative addition to become Rh(III) (d⁶, 18e⁻).

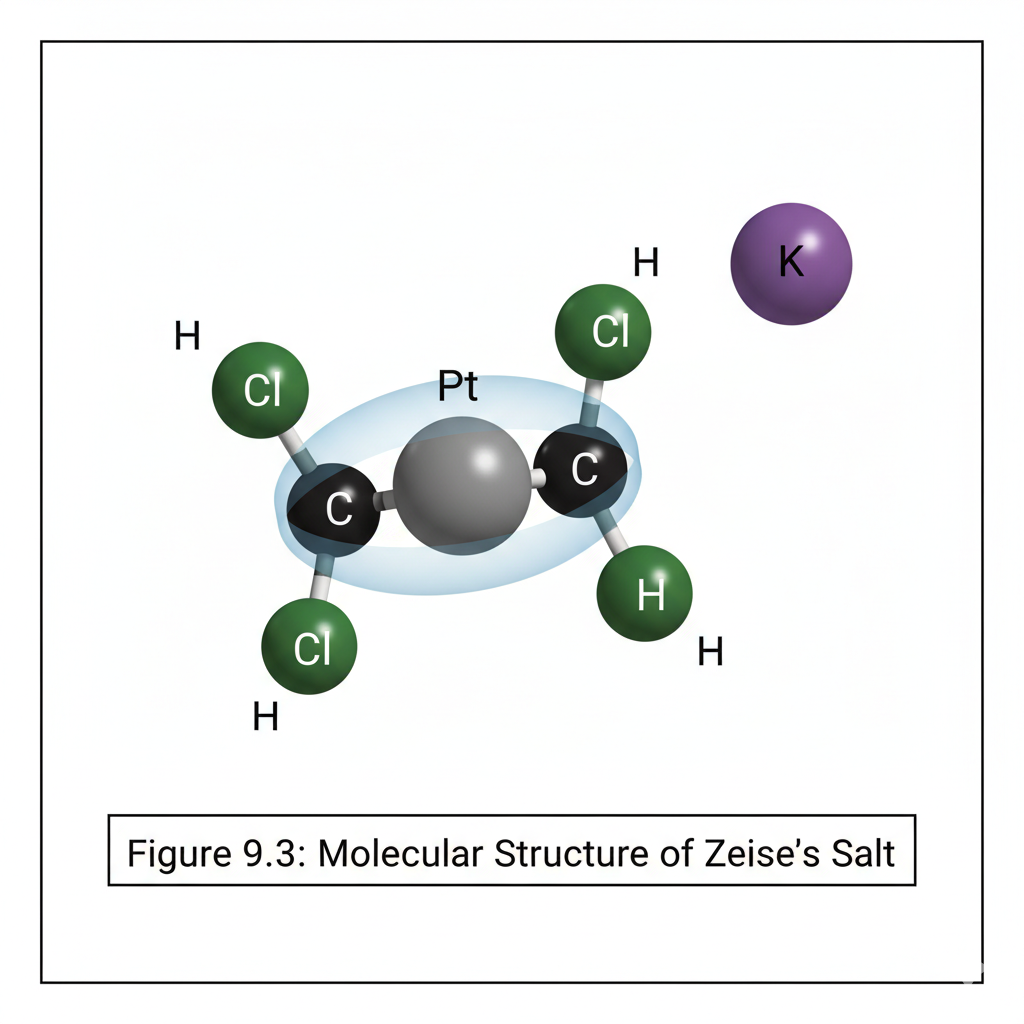
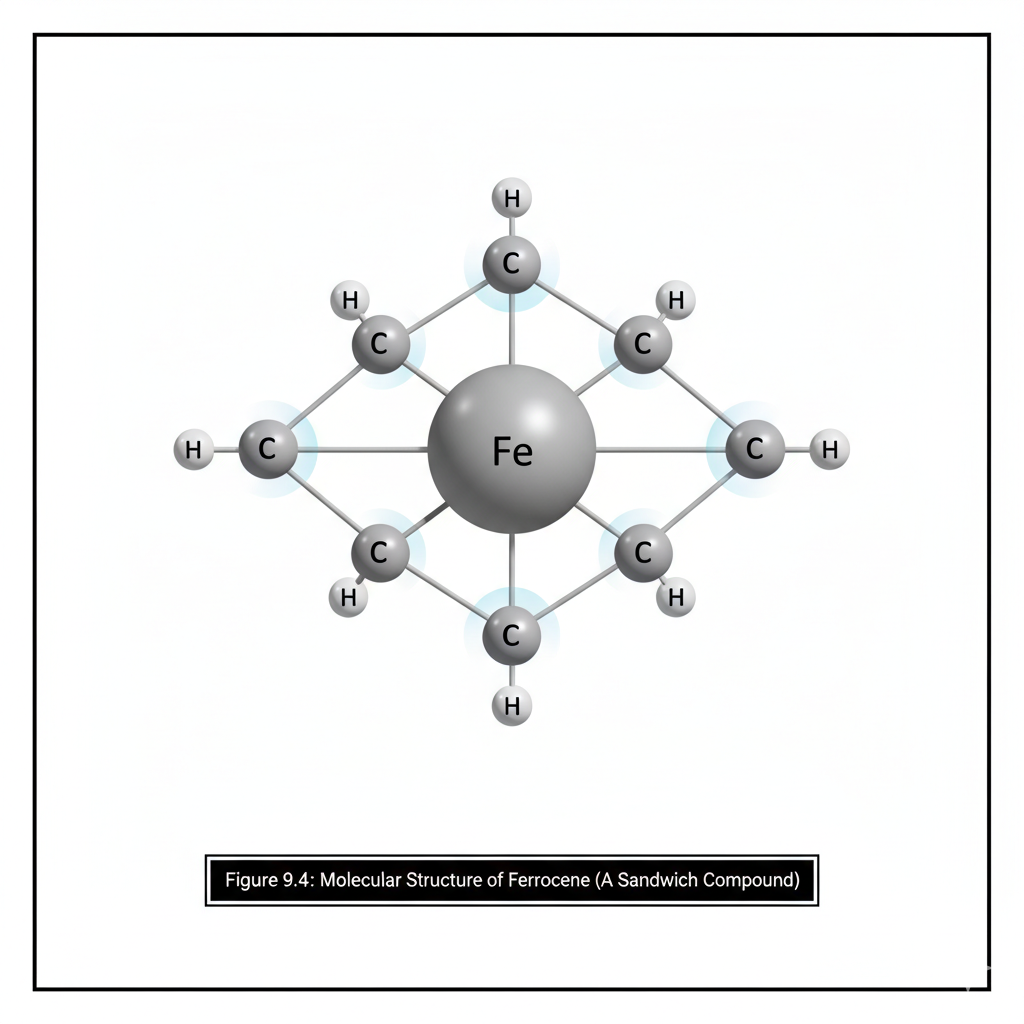
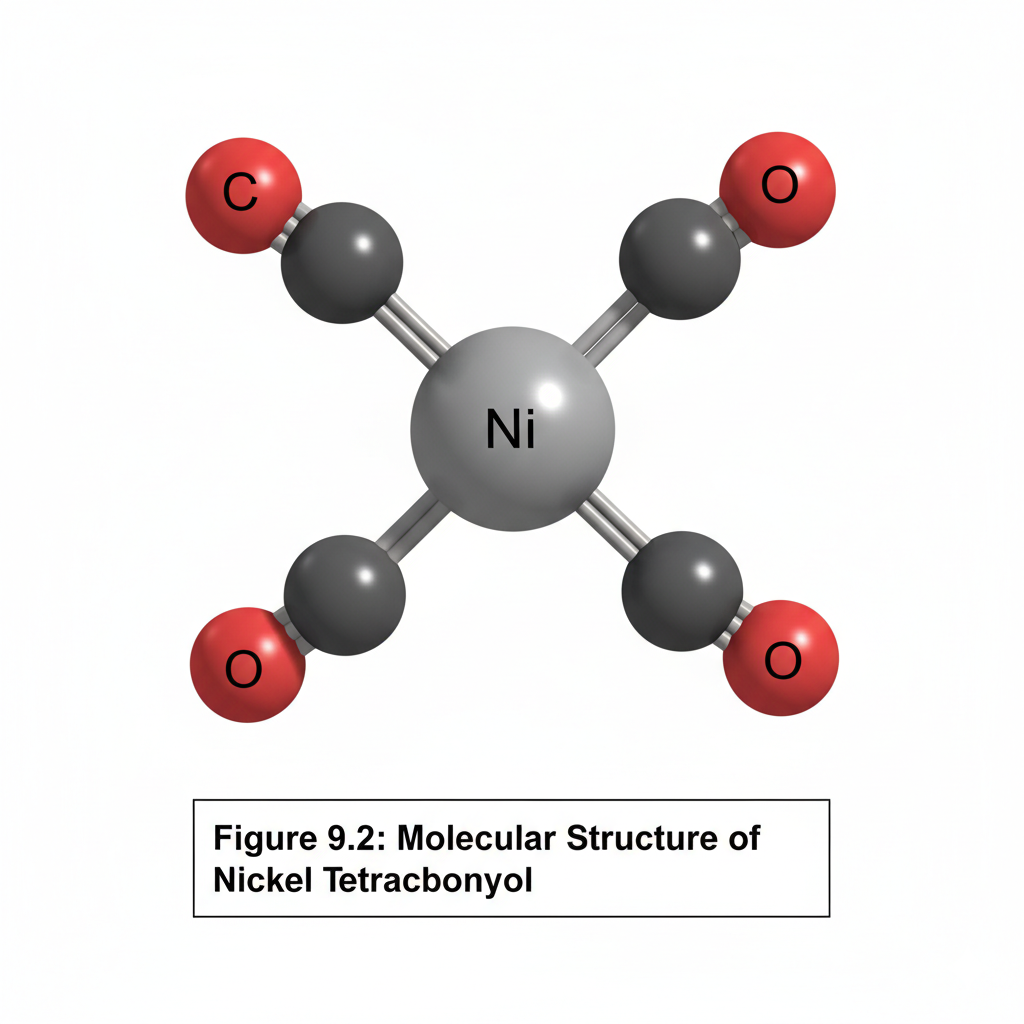
Reductive Elimination (RE):The reverse of oxidative addition. Two ligands on the metal center couple together and depart as a new molecule, decreasing the metal's oxidation state by -2 and its coordination number by -2. This typically occurs from higher oxidation states and forms a stable organic product.
- General form: A-Mⁿ⁺²-B → Mⁿ + A-B
- Practical Example: The formation of acetyl iodide from a rhodium(III) complex in the Monsanto acetic acid process.
  [Rh(CO)₂I₃(COCH₃)]⁻ → [Rh(CO)₂I₂]⁻ + CH₃COI
  Here, Rh(III) (d⁶, 18e⁻) undergoes reductive elimination to regenerate Rh(I) (d⁸, 16e⁻) and release the product.
Migratory Insertion (or simply Insertion):A ligand (e.g., an alkyl group) migrates from the metal to an adjacent unsaturated ligand (e.g., CO, alkene), forming a new C-C bond and reducing the coordination number by one. The metal's oxidation state remains unchanged. A vacant coordination site is created.
- General form: R-M-X → M-(R-X) (where R moves to X)
- Practical Example: The insertion of carbon monoxide into a metal-methyl bond in the Monsanto acetic acid process.
  [Rh(CO)₂I₃(CH₃)]⁻ → [Rh(CO)I₃(COCH₃)]⁻
  The methyl group migrates to a coordinated CO, forming an acetyl ligand (COCH₃). This creates a vacant site, and another CO can then bind to the Rh center.

Chapter 10: Solid-State Inorganic Chemistry and Materials Science

Solid-state inorganic chemistry and materials science represent a vast and incredibly important field, underpinning much of our modern technological world. From the microchips in our computers to the catalysts that enable industrial processes and the advanced ceramics in aerospace, the design and understanding of solid materials are paramount. This chapter delves into the fundamental principles governing the structures and properties of these fascinating substances.

10.1 Types of Solids and Their Characteristic Features

Solids are characterized by their rigid structure and fixed shape, a consequence of strong intermolecular or interatomic forces. We can broadly classify solids into four main types based on the nature of these forces:

Ionic Solids:These solids are composed of oppositely charged ions held together by strong electrostatic forces. They typically form crystalline lattices where each ion is surrounded by ions of the opposite charge.
- Characteristic features: High melting and boiling points, hard and brittle, poor electrical conductors in the solid state (because ions are fixed) but good conductors when molten or dissolved (as ions become mobile). They are often soluble in polar solvents.
- Practical Example: Sodium chloride (NaCl), common table salt. In its solid form, NaCl forms a cubic crystal lattice. When melted or dissolved in water, the Na⁺ and Cl⁻ ions dissociate, allowing for electrical conductivity.
Covalent Network Solids:In these materials, atoms are linked together by strong covalent bonds extending throughout the entire structure, forming a giant molecule or network.
- Characteristic features: Extremely hard, very high melting points, typically poor electrical conductors (with some notable exceptions like graphite). They are usually insoluble in common solvents.
- Practical Example: Diamond, a pure carbon allotrope. Each carbon atom is sp³ hybridized and covalently bonded to four other carbon atoms in a tetrahedral arrangement, creating an incredibly strong and rigid network. This makes diamond the hardest known natural material. Another example is silicon dioxide (SiO₂), the main component of quartz, where silicon atoms are covalently bonded to oxygen atoms.
Molecular Solids:These solids consist of discrete molecules held together by weaker intermolecular forces (van der Waals forces, dipole-dipole interactions, hydrogen bonding). The atoms within each molecule are covalently bonded.
- Characteristic features: Relatively low melting and boiling points, soft, poor electrical conductors. They can be soluble in nonpolar solvents or, if polar, in polar solvents.
- Practical Example: Ice (solid H₂O). Water molecules are held together by hydrogen bonds, which are stronger than typical van der Waals forces but much weaker than covalent or ionic bonds. This explains ice's relatively low melting point compared to ionic or covalent network solids. Dry ice (solid CO₂) is another example, where CO₂ molecules are held by weak van der Waals forces, leading to sublimation at −78.5 °C.
Metallic Solids:These solids are composed of metal atoms arranged in a crystal lattice. The valence electrons are delocalized and form a "sea of electrons" that surrounds a lattice of positive metal ions.
- Characteristic features: Good electrical and thermal conductors, malleable (can be hammered into sheets), ductile (can be drawn into wires), lustrous. They have a wide range of melting points.
- Practical Example: Copper wire. The delocalized electrons in copper allow for easy flow of charge, making it an excellent electrical conductor. The ability of the electron sea to adapt to changes in the metal ion positions without breaking the overall bonding explains copper's malleability and ductility.

10.2 Crystal Structures and Unit Cells

Most solids, particularly inorganic ones, exhibit a highly ordered, repeating arrangement of atoms, ions, or molecules known as a crystal lattice. The smallest repeating unit that generates the entire crystal when translated in three dimensions is called the unit cell. Understanding unit cells is crucial for predicting and explaining material properties.

Simple Cubic (SC): Atoms at each corner of a cube.
Body-Centered Cubic (BCC):Atoms at each corner and one in the center of the cube.
- Practical Example: Iron (Fe) at room temperature adopts a BCC structure.
Face-Centered Cubic (FCC) or Cubic Close-Packed (CCP):Atoms at each corner and one in the center of each face of the cube.
- Practical Example: Copper (Cu), aluminum (Al), and gold (Au) all crystallize in an FCC structure. This close-packed arrangement contributes to their ductility.
Hexagonal Close-Packed (HCP):A non-cubic close-packed structure.
- Practical Example: Zinc (Zn) and magnesium (Mg) exhibit HCP structures.

Beyond simple elemental structures, many inorganic compounds form more complex crystal structures:

NaCl Structure:A face-centered cubic arrangement of anions (e.g., Cl⁻) with cations (e.g., Na⁺) occupying all octahedral interstitial sites. Conversely, it can be viewed as an FCC array of cations with anions in the octahedral holes.
- Practical Example: Sodium chloride (NaCl), Lithium fluoride (LiF).
CsCl Structure:A simple cubic arrangement of one type of ion (e.g., Cl⁻) with the other ion (e.g., Cs⁺) at the body center of the cube.
- Practical Example: Cesium chloride (CsCl).
Perovskite Structure (ABO₃):A critically important structure in materials science. It typically features a larger cation (A) at the corners, a smaller cation (B) at the body center, and oxygen anions (O) at the face centers of a cubic unit cell.
- Practical Example: Barium titanate (BaTiO₃) is a classic perovskite, widely used in capacitors and piezoelectric devices due to its ferroelectric properties. High-temperature superconductors often have perovskite-related structures.

10.3 Defects in Solids and Non-Stoichiometry

Real crystals are rarely perfect. Defects are deviations from the ideal crystal structure and play a profound role in influencing material properties.

Inorganic Chemistry chemistry engineering science technology physics

INORGANIC CHEMISTRY

Inorganic Chemistry

Course Description:

Course Objectives:

Chapter 2: Periodic Trends and Chemical Bonding

Chapter 3: Molecular Symmetry and Group Theory

Chapter 4: Acid-Base Chemistry in Inorganic Systems

Chapter 5: Chemistry of Main Group Elements I (Groups 1, 2, 13, 14)

Chapter 6: Chemistry of Main Group Elements II (Groups 15, 16, 17, 18)

Chapter 7: Introduction to Transition Metal Chemistry and Ligand Field Theory

Chapter 8: Coordination Chemistry: Structure, Isomerism, and Reactivity

Chapter 9: Organometallic Chemistry: Fundamentals and Applications

Chapter 10: Solid-State Inorganic Chemistry and Materials Science

Chapter 2: Periodic Trends and Chemical Bonding

Periodic Trends: Unveiling the Patterns

Atomic and Ionic Radii

Ionization Energy

Electron Affinity

Electronegativity

Chemical Bonding: The Glue That Holds Matter Together

Ionic Bonding

Covalent Bonding

Metallic Bonding

Intermolecular Forces: Shaping Bulk Properties

Types of Intermolecular Forces

Conclusion

Chapter 3: Molecular Symmetry and Group Theory

Symmetry Elements and Operations

Point Groups

Basics of Group Theory

Character Tables and Irreducible Representations

Applications of Symmetry

Chapter 4: Acid-Base Chemistry in Inorganic Systems

1. Review of Traditional Acid-Base Theories

1.1 Brønsted-Lowry Theory

1.2 Lewis Acid-Base Theory

2. Expanded Acid-Base Concepts for Inorganic Systems

2.1 Lux-Flood Theory

2.2 Usanovich Theory

2.3 Solvent System Theory

3. Hard and Soft Acids and Bases (HSAB) Theory

3.1 Definitions of Hard and Soft

3.2 Principles and Applications of HSAB Theory

Conclusion

Chapter 5: Chemistry of Main Group Elements I (Groups 1, 2, 13, 14)

Group 1: The Alkali Metals (Li, Na, K, Rb, Cs, Fr)

Group 2: The Alkaline Earth Metals (Be, Mg, Ca, Sr, Ba, Ra)

Group 13: The Boron Group (B, Al, Ga, In, Tl)

Group 14: The Carbon Group (C, Si, Ge, Sn, Pb)

Chapter 6: Chemistry of Main Group Elements II (Groups 15, 16, 17, 18)

Group 15: The Nitrogen Group (Pnictogens)

Group 16: The Chalcogens

Group 17: The Halogens

Group 18: The Noble Gases

Geometries of Coordination Complexes

Isomerism in Coordination Compounds

Reactivity of Coordination Complexes

Chapter 9: Organometallic Chemistry: Fundamentals and Applications

The Nature of the Metal-Carbon Bond

Common Organometallic Ligands

The 18-Electron Rule

Key Reactions in Organometallic Chemistry